[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 2 3 4 5 6 7
[2,] 3 4 5 6 7 8
[3,] 4 5 6 7 8 9
[4,] 5 6 7 8 9 10
[5,] 6 7 8 9 10 11
[6,] 7 8 9 10 11 12Bayesian Inference
NYU Applied Statistics for Social Science Research
Introductions
- State your name
- What is your field of study/work, and what are you hoping to learn in this class
- Go to: https://tinyurl.com/nyu-colab and write down where you are from (Country, City)

\[ \DeclareMathOperator{\E}{\mathbb{E}} \DeclareMathOperator{\P}{\mathbb{P}} \DeclareMathOperator{\V}{\mathbb{V}} \DeclareMathOperator{\L}{\mathscr{L}} \DeclareMathOperator{\I}{\text{I}} \DeclareMathOperator{\d}{\mathrm{d}} \]
Lecture 1: Bayesian Workflow
- Overview of the course
- Class participation: prediction intervals
- Statistics vs AI/ML
- Brief history of Bayesian inference
- Stories: pricing books and developing drugs
- Review of probability and simulations
- Bayes’s rule
- Introduction to Bayesian workflow
- Wanna bet? Mystery box game

Statistics vs. AI/ML (Simplification!)
- AI is about automating tasks that humans are able to to
- Recognizing faces, cats, and other objects
- Identifying tumors on a radiology scan
- Playing Chess and Go
- Driving a car
- Post ChatGPT 4: Generating coherent text/images/video, signs of reasoning
- Statistics is useful for answering questions that humans are not able to do
- How fast does a drug clear from the body?
- What is the expected tumor size two months after treatment?
- How would patients respond under a different treatment?
- Should I take this drug?
- Should we (FDA/EMA/…) approve this drug?
Note
“Machine learning excels when you have lots of training data that can be reasonably modeled as exchangeable with your test data; Bayesian inference excels when your data are sparse and your model is dense.” — Andrew Gelman
Turn to your neighbor and discuss
Classify each of the following: {decision, parameter inference, prediction, causal inference}
- How fast does a drug clear from the body?
- What is the expected tumor size two months after treatment?
- How would patients respond under a different treatment?
- Should I take this drug?
- Should we (FDA/EMA/…) approve this drug?

Question
Which category is missing data imputation?
Brief History
Summary of the book The Theory That Would Not Die
- Thomas Bayes (1702(?) — 1761) is credited with the discovery of the “Bayes’s Rule”
- His paper was published posthumously by Richard Price in 1763
- Laplace (1749 — 1827) independently discovered the rule and published it in 1774
- Scientific context: Newton’s Principia was published in 1687
- Bayesian wins: German Enigma cipher, search for a missing H-bomb, Federalist papers, Moneyball, FiveThirtyEight

Laplace’s Demon
We may regard the present state of the universe as the effect of its past and the cause of its future. An intellect which at any given moment knew all of the forces that animate nature and the mutual positions of the beings that compose it, if this intellect were vast enough to submit the data to analysis, could condense into a single formula the movement of the greatest bodies of the universe and that of the lightest atom; for such an intellect nothing could be uncertain, and the future just like the past would be present before its eyes.

Marquis Pierre Simon de Laplace (1729 — 1827)
“Uncertainty is a function of our ignorance, not a property of the world.”
Modern Examples of Bayesian Analyses


Left: Pierre Simon Laplace in the style of Wassily Kandinsky, by OpenAI DALL·E
Elasticity of Demand
Stan with Hierarchical Models
Pharmacokinetics of Drugs
Stan with Ordinary Differential Equations
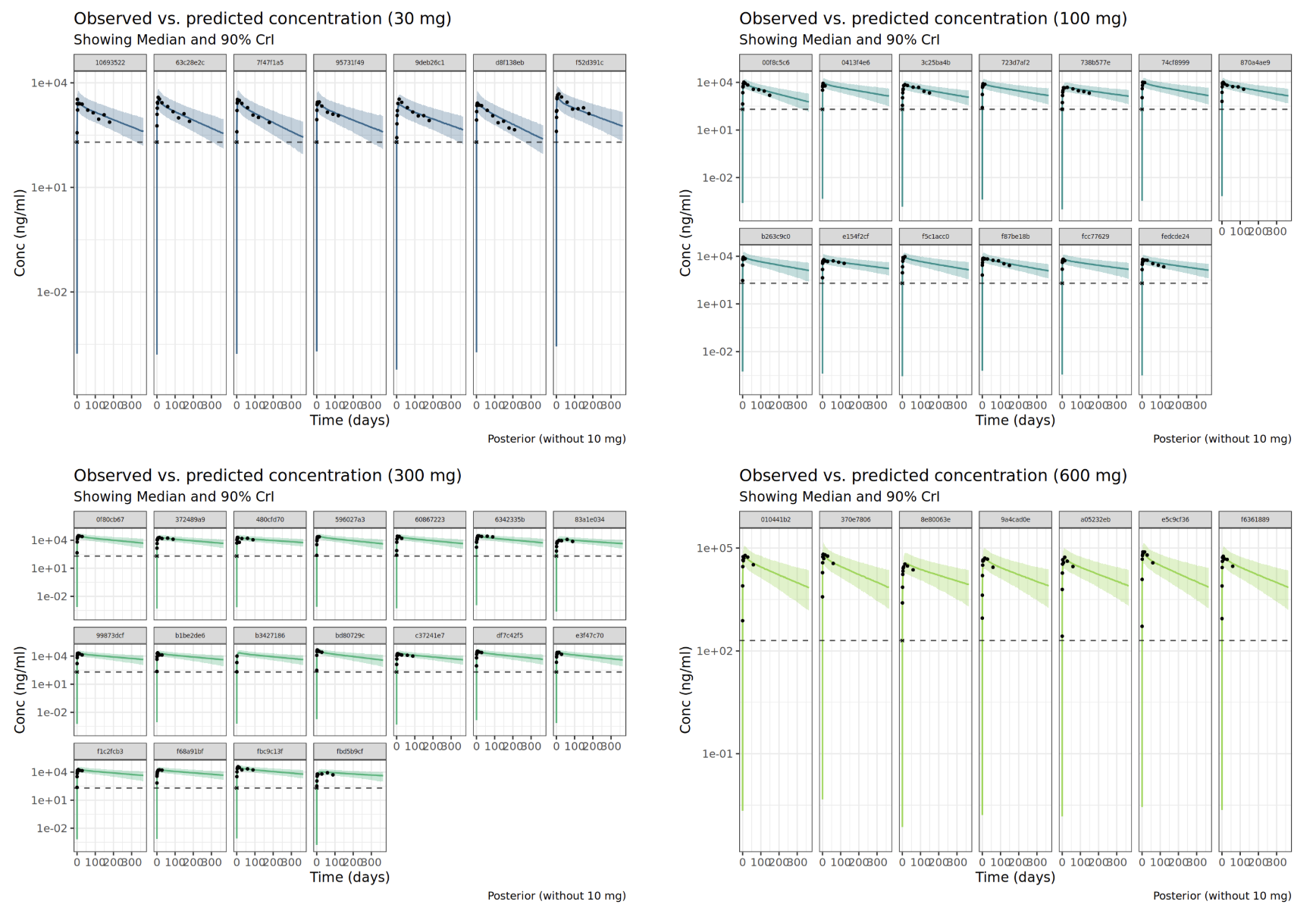
Nonparametric Bayes
Stan with Gaussian Processes
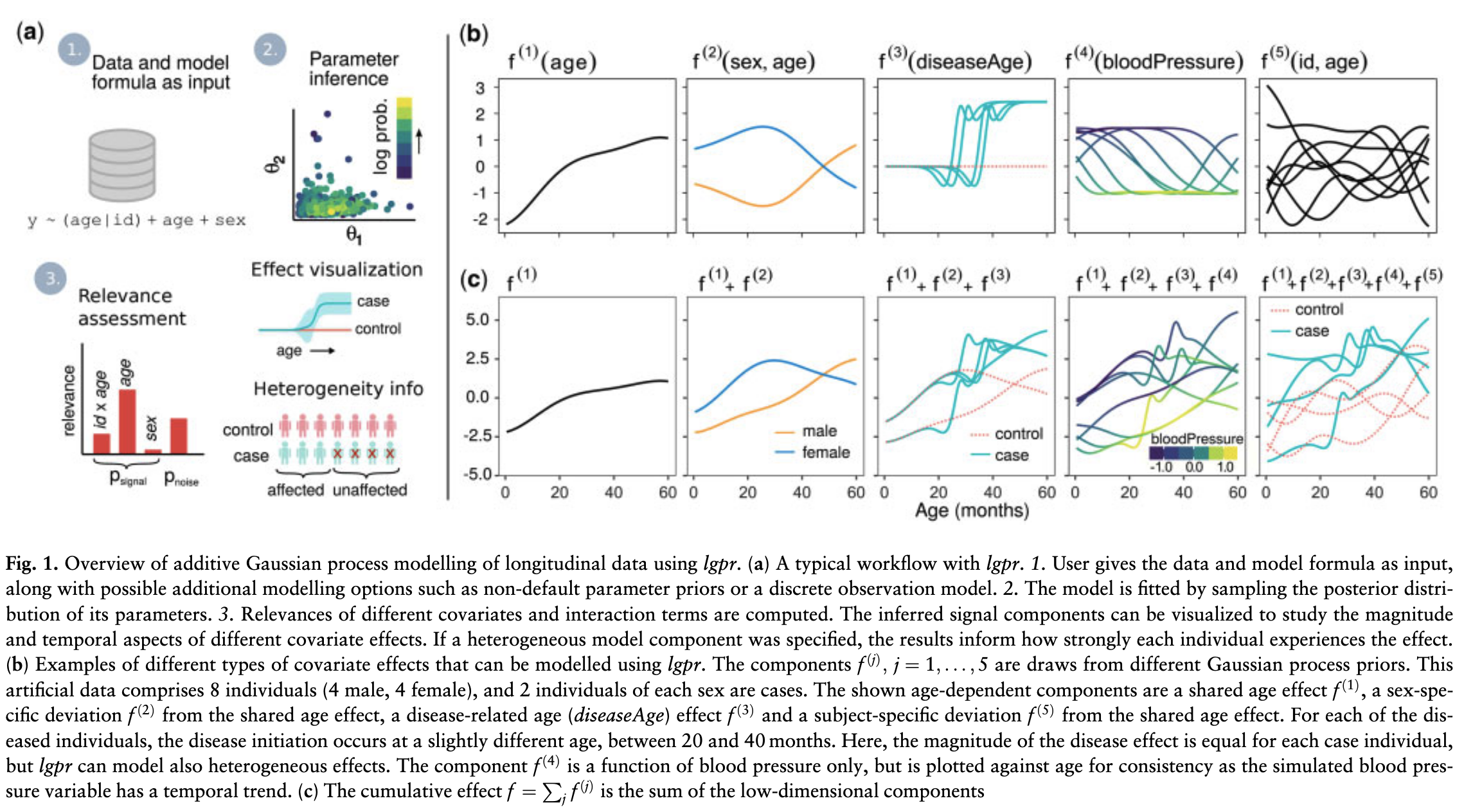
Timonen, J., Mannerström, H., Vehtari, A., & Lähdesmäki, H. (2021)
Review of Probability
- A set of all possible outcomes: \(\Omega\)
- An outcome of an experiment: \(\omega \in \Omega\)
- We typically denote events by capital letters, say \(A \subseteq \Omega\)
- Axioms of probability:
- Non-negativity: \(\P(A) \geq 0, \, \text{for all } A\)
- Normalization: \(\P(\Omega) = 1\)
- Additivity: If \(A_1, A_2, A_3, \ldots\) are disjoint, \(\P(\cup_{i=1}^{\infty} A_i) = \sum_{i=1}^{\infty} \P(A_i)\)
Random Variables Review
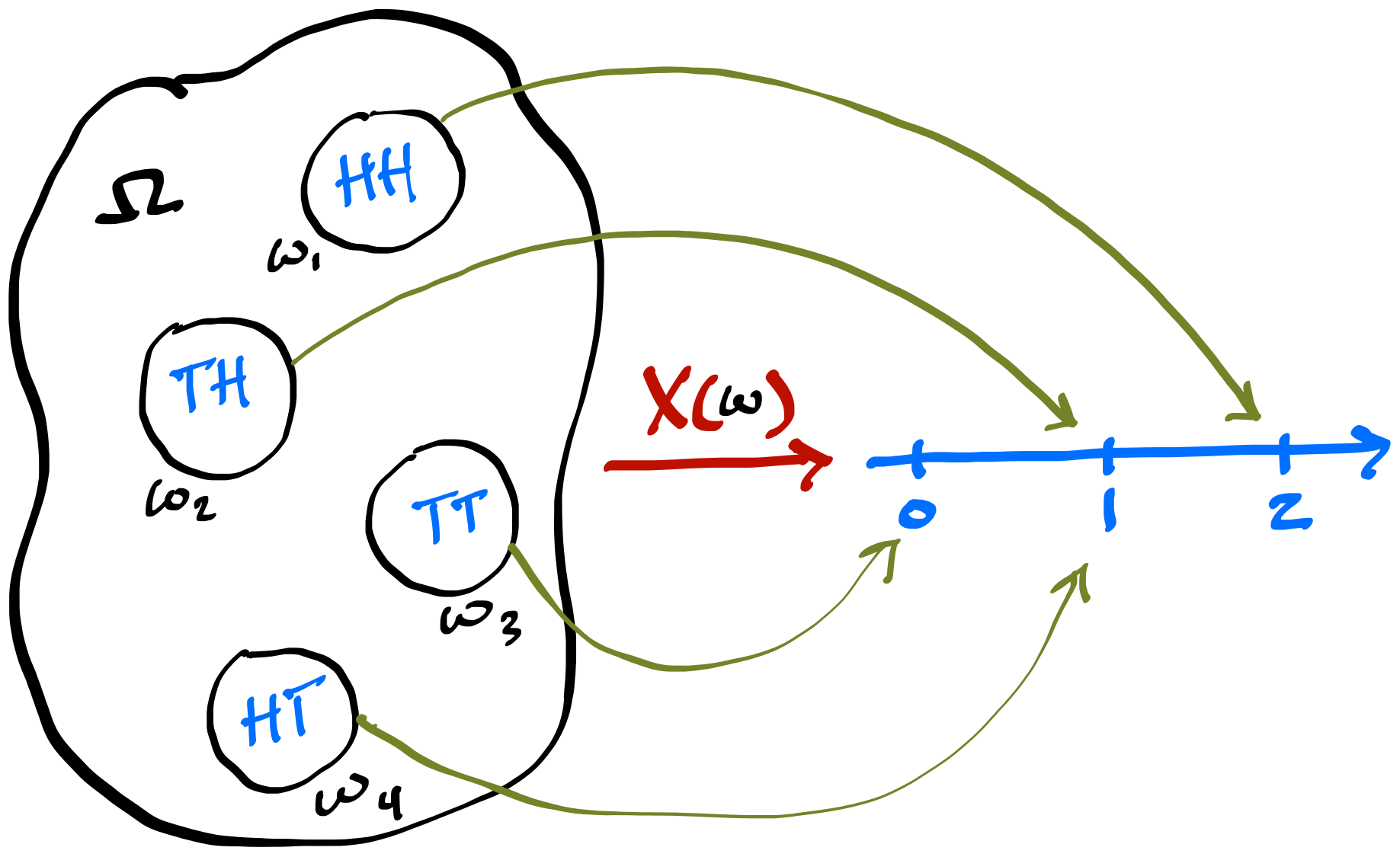
- A random variable \(X\) is a function that maps outcomes of a random experiment to real numbers. \(X: \Omega \to \mathbb{R}\). For each \(\omega \in \Omega\), \(X(\omega) \in\mathbb{R}\).
\[ \P_X(X = x_i) = \P\left(\{\omega_j \in \Omega : X(\omega_j) = x_i\}\right) \]
- PMF, PDF, CDF (Blitzstein and Hwang, Ch. 3, 5)
- Expectations (Blitzstein and Hwang, Ch. 4)
- Joint Distributions (Blitzstein and Hwang, Ch. 7)
- Conditional Expectations (Blitzstein and Hwang, Ch. 9)
Random variable \(X(\omega)\) for the number of Heads in two flips
Example
- You roll a fair six-sided die twice
- Give an example of an \(\omega \in \Omega\)
- How many elements are in \(\Omega\)? What is \(\Omega\)?
- Define an event \(A\) as the sum of the two rolls less than 11
- How many elements are in \(A\)?
- What is \(\P(A)\)?
- \(\Omega\) consists of all pairs:
- \(\{(1, 1), (1, 2), ... (2, 1), (2, 2), ...\}\)
- There are 36 such pairs
- 33 of those pairs result in a sum of less than 11
- \(\P(A) = \frac{33}{36} = \frac{11}{12} \approx 0.917\)
Example Simulation
- We will use R’s
sample()function to simulate rolls of a die andreplicate()function to repeat the rolling process many times
[1] 3 2 [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
X1 2 6 2 4 6 1 2 1 1 4
X2 4 6 4 4 2 4 4 6 4 5[1] 6 12 6 8 8 5[1] 0.915- Given a Random Variable \(Y\), \(y^{(1)}, y^{(2)}, y^{(3)}, \ldots, y^N\) are simulations or draws from \(Y\)
- Fundamental bridge (Blitzstein & Hwang p. 164): \(\P(A) = \E(\I_A)\)
- For \(Y = X_1 + X_2\): \(\P(Y < 11) \approx \frac{1}{N} \sum^{N}_{n=1} \I(y^n < 11)\)
- In R, \(Y < 11\) creates an indicator variable
- And
mean()does the average
Warning
There is something sublte going on: a difference between generating 100 draws from one random variable \(Y\) vs getting one draw from 100 \(Y\)s
Example Simulation
This is a more direct demonstration of random draws from a distribution of \(Y = X_1 + X_2\)
CDF, PDF, and Inverse CDF
- The CDF of a random variable \(X\) is defined as: \[ F_X(x) = \P(X \leq x) \\ 0 \leq F_X(x) \leq 1 \quad \\ \lim_{x \to -\infty} F_X(x) = 0 \text{ and } \lim_{x \to \infty} F_X(x) = 1 \]
- The PDF of a random variable \(X\) with differentiable \(F_X(x)\) \[ f_X(x) = \frac{\d}{\text{d}x}F_X(x) \\ f_X(x) \geq 0 \quad \\ \int_{-\infty}^\infty f_X(x) \, \text{d}x = 1, \text{ and } \int_{x \in A} f_X(x) \ \text{d}x = \P(X \in A) \]
- The quantile function of a random variable \(X\) is defined as: \[ Q_X(p) = F_X^{-1}(p), \, p \in [0, 1] \]
Bivariate Case
- A bivariate CDF \(F_{X,Y}(x, y) = \P(X \leq x, Y \leq y)\)
\[ F_{X,Y}(x, y) \geq 0 \quad \text{for all } x, y \]
- If the PDF exists
\[ F_{X,Y}(x, y) = \int_{-\infty}^x \int_{-\infty}^y f_{X,Y}(u, v) \, \mathrm{d}v \, \mathrm{d}u \]
- Normalization
\[ \int_{-\infty}^\infty \int_{-\infty}^\infty f_{X,Y}(x, y) \, \mathrm{d}x \, \mathrm{d}y = 1 \]
- From CDF to PDF
\[ f_{X,Y}(x, y) = \frac{\partial^2}{\partial x \partial y} F_{X,Y}(x, y) \]
Bivariate Case
- Marginalization
\[ f_Y(y) = \int_{-\infty}^\infty f_{X,Y}(x, y) \, \mathrm{d}x. \]
- Conditional CDF
\[ F_{Y \mid X}(y \mid x) = \P(Y \leq y \mid X = x) \]
- Conditional PDF: a function of \(y\) for fixed \(x\) \[ f_{Y|X}(y \mid x) = \frac{f_{X,Y}(x, y)}{f_X(x)} \]
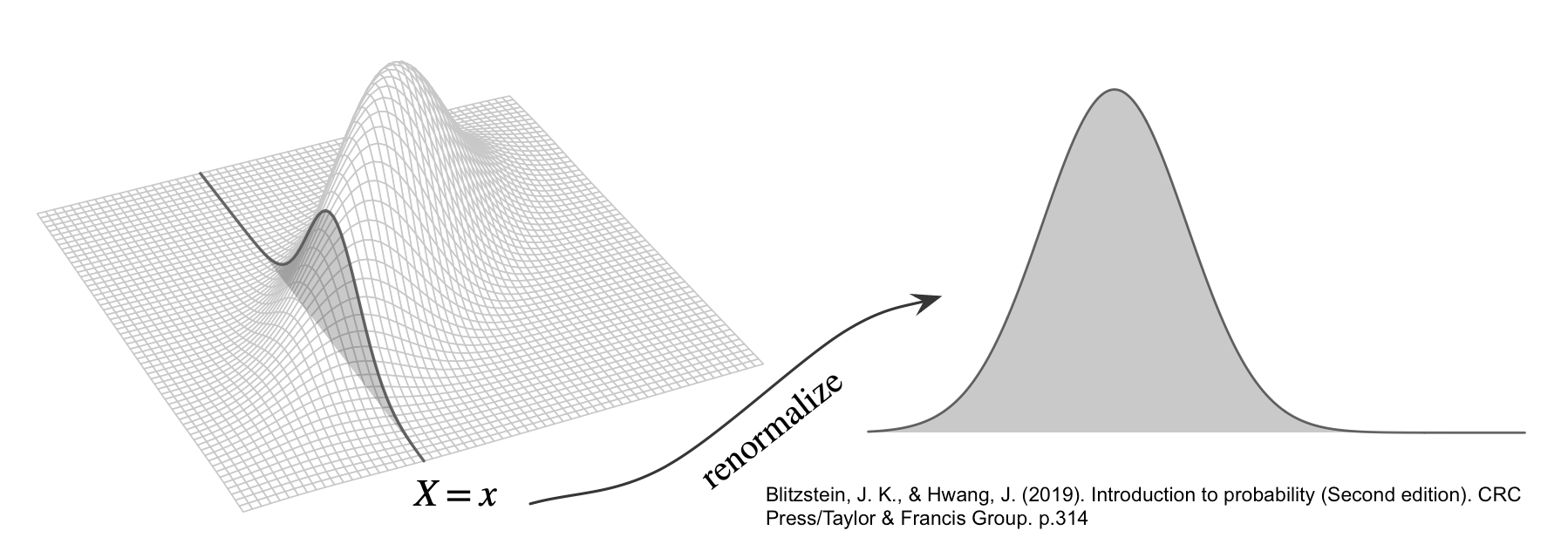
Bivariate Normal
\[ f_{X,Y}(x, y) = \frac{1}{2 \pi \sqrt{\det(\Sigma)}} \exp\left( -\frac{1}{2} \begin{bmatrix} x - \mu_X \\ y - \mu_Y \end{bmatrix}^\top \Sigma^{-1} \begin{bmatrix} x - \mu_X \\ y - \mu_Y \end{bmatrix} \right) \]
Bivariate Normal Demo
library(distributional)
sigma_X <- 1
sigma_Y <- 2
rho <- 0.3 # Correlation coefficient
rho_sigmaXY <- rho * sigma_X * sigma_Y # why?
cov_matrix <- matrix(c(sigma_X^2, rho_sigmaXY,
rho_sigmaXY, sigma_Y^2), 2, 2)
dmv_norm <- dist_multivariate_normal(mu = list(c(0, 0)),
sigma = list(cov_matrix))
dimnames(dmv_norm) <- c("x", "y")
variance(dmv_norm) x y
[1,] 1 4[[1]]
x y
[1,] 1.0 0.6
[2,] 0.6 4.0[1] 0[1] 0.93List of 1
$ : num [1:10000, 1:2] 0.0231 2.2418 0.9219 0.0766 -1.0797 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : NULL
.. ..$ : chr [1:2] "x" "y"# A tibble: 6 × 2
x y
<dbl> <dbl>
1 0.0231 1.74
2 2.24 2.25
3 0.922 0.556
4 0.0766 -3.37
5 -1.08 -0.600
6 0.0373 -1.41 x y
-0.01 -0.03 x y
x 0.99 0.61
y 0.61 4.06 x y
x 1.0 0.3
y 0.3 1.0[1] 0.93[1] 0.81How would we do the above analytically? \[ \P(X < 0 \cup Y < 1) = \P(X < 0) + \P(Y < 1) - \P(X < 0 \cap Y < 1) \]
# Compute P(X < 0)
p_X_less_0 <- cdf(dist_normal(mu = 0, sigma = sigma_X), 0) # pnorm(0, mean = 0, sd = sigma_X)
# Compute P(Y < 1)
p_Y_less_1 <- cdf(dist_normal(mu = 0, sigma = sigma_Y), 1) # pnorm(1, mean = 0, sd = sigma_Y)
# Compute P(X < 0, Y < 1)
p_X_less_0_and_Y_less_1 <- cdf(dmv_norm, cbind(0, 1))
# P(X < 0 or Y < 1)
(p_X_less_0 + p_Y_less_1 - p_X_less_0_and_Y_less_1) |> round(2)[1] 0.8- Whould you rather do
mean(draws$x < 0 | draws$y < 1)or the analytical solution? - How would you evaluate \(\P(X < 0 \mid Y < 1)\)
Review of Conditional Probability
- For arbitrary \(A\) and \(B\), if \(\P(B) > 0\):
- Conditional probability: \(\P(A \mid B) = \frac{\P(AB)}{\P(B)}\)
- Conditional probability: \(\P(B \mid A) = \frac{\P(AB)}{\P(A)}\)
- Bayes’s rule: \(\P(A \mid B) = \frac{\P(AB)}{\P(B)} = \frac{\P(B \mid A) \P(A)}{\P(B)}\)
- \(A\) and \(B\) are independent if observing \(B\) does not give you any more information about \(A\): \(\P(A \mid B) = \P(A)\)
- And \(\P(A B) = \P(A) \P(B)\) (from Bayes’s rule)
Joint, Marginal, and Conditional
- Titanic carried approximately 2,200 passengers and sank on 15 April 1912
- Let \(G: \{m, f\}\) represent Gender and \(S: \{n, y\}\) represent Survival
| Sex | No | Yes | Total |
|---|---|---|---|
| Male | 0.620 | 0.167 | 0.787 |
| Female | 0.057 | 0.156 | 0.213 |
| Total | 0.677 | 0.323 | 1.000 |
- \(\P(G = m \cap S = y) =\) 0.167
- \(\P(S = y) = \sum_{i \in \{m, f\}} \P(S = y \, \cap G = i) =\) ??
- \(\P(S = y) = \sum_{i \in \{m, f\}} \P(S = y \, \cap G = i) = 0.323\)
Joint, Marginal, and Conditional
- What is \(\P(G = m \mid S = y)\), probability of being
male given survival? - To compute that, we only consider the column
where Survival = Yes - \(\P(G = m \mid S = y) = \frac{\P(G = m \, \cap \, S = y)}{\P(S = y)} = \frac{0.167}{0.323} \\ \approx 0.52\)
- You want \(\P(S = y \mid G = m)\), comparing it to \(\\ \qquad \ \ \ \ \ \ \P(S = y \mid G = f)\)
- \(\P(S = y \mid G = m) = \frac{\P(G = m \, \cap \, S = y)}{\P(G = m)} = \frac{0.167}{0.787} \\ \approx 0.21\)
- \(\P(S = y \mid G = f) = \frac{\P(G = f \, \cap \, S = y)}{\P(G = f)} = \frac{0.156}{0.213} \\ \approx 0.73\)
- How would you compute \(\P(S = n \mid G = m)\)?
- \(\P(S = n \mid G = m) = 1 - \P(S = y \mid G = m)\)
| Sex | No | Yes | Total |
|---|---|---|---|
| Male | 0.620 | 0.167 | 0.787 |
| Female | 0.057 | 0.156 | 0.213 |
| Total | 0.677 | 0.323 | 1.000 |
 “Untergang der Titanic”, as conceived by Willy Stöwer, 1912
“Untergang der Titanic”, as conceived by Willy Stöwer, 1912
Law of Total Probability (LOTP)
Let \(A\) be a partition of \(\Omega\), so that each \(A_i\) is disjoint, \(\P(A_i >0)\), and \(\cup A_i = \Omega\). \[ \P(B) = \sum_{i=1}^{n} \P(B \cap A_i) = \sum_{i=1}^{n} \P(B \mid A_i) \P(A_i) \]
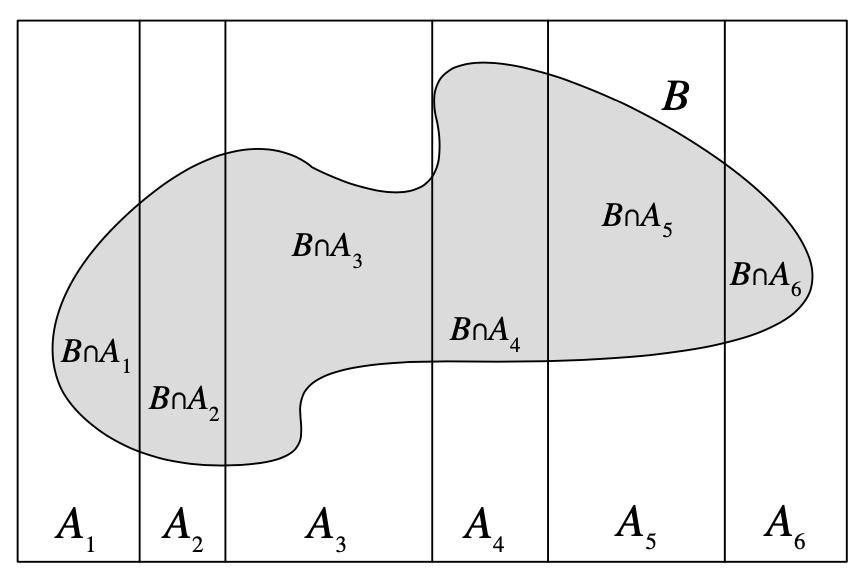
Image from Blitzstein and Hwang (2019), Page 55
Bayes’s Rule
- Bayes’s rule for events
\[ \P(A \mid B) = \frac{\P(A \cap B)}{\P(B)} = \frac{\P(B \mid A) \P(A)}{\sum_{i=1}^{n} \P(B \mid A_i) \P(A_i)} \]
- Bayes’s rule for continuous RVs
\[ \underbrace{\color{blue}{f_{\Theta|Y}(\theta \mid y)}}_{\text{Posterior}} = \frac{ \overbrace{ \color{red}{f_{Y|\Theta}(y \mid \theta)} }^{\text{Likelihood}} \cdot \overbrace{\color{green}{f_\Theta(\theta)}}^{ \text{Prior} } }{ \underbrace{\int_{-\infty}^{\infty} f_{Y|\Theta}(y \mid \theta) f_\Theta(\theta) \, \text{d}\theta}_{\text{Prior Predictive } f(y)} } \propto \color{red}{f_{Y|\Theta}(y \mid \theta)} \cdot \color{green}{f_\Theta(\theta)} \]
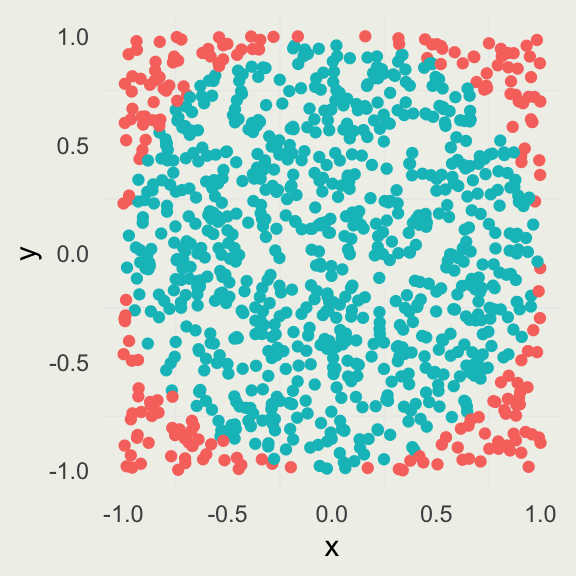
Estimating \(\pi\) by Simulation
- \(A_c\): area of a circle with radius \(r\)
- \(A_s\): area of a square with the side \(2r\)
\[ \begin{align} A_{c}& = \pi r^2 \\ A_{s}& = (2r)^2 = 4r^2 \\ \frac{A_{c}}{A_{s}}& = \frac{\pi r^2}{4r^2} = \frac{\pi}{4} \implies \pi = \frac{4A_{c}}{A_{s}} \end{align} \]
Estimating \(\pi\) by Simulation
To estimate \(\pi\), we perform the following simulation:
\[ \begin{align} X& \sim \text{Uniform}(-1, 1) \\ Y& \sim \text{Uniform}(-1, 1) \\ \pi& \approx \frac{4 \sum_{i=1}^{N} \I(x_i^2 + y_i^2 < 1)}{N} \end{align} \]
The numerator is a sum over an indicator function \(\I\), which evaluates to \(1\) if the inequality holds and \(0\) otherwise.
Estimating \(\pi\) by Simulation
Simplified Notation
- \(\theta\): unknowns or parameters to be estimated; could be multivariate, discrete, and continuous; in your book \(\pi\)
- \(y\): observations or measurements to be modelled (\(y_1, y_2, ...\))
- \(\widetilde{y}\) : unobserved but observable quantities; in your book \(y'\)
- \(x\): covariates
- \(f( \theta )\): a prior model, P[DM]F of \(\theta\)
- \(f(y \mid \theta, x)\): an observational model, P[DM]F when it is a function of \(y\); in your book: \(f(y \mid \pi)\)
- \(f(y \mid \theta)\): is a likelihood function when it is a function of \(\theta\); in your book: \(\L(\pi \mid y)\)
- Some people write \(\L(\theta; y)\) or simply \(\L(\theta)\)
- \(U(z)\): utility function where \(z\) can be \(\theta\), \(\tilde{y}\)
- \(\E(U(z) \mid d)\): expected utility for decision \(d\)
Simplified Bayesian Workflow
- Specify a prior model \(f(\theta)\)
- Pick a data model \(f(y \mid \theta, x)\), including conditional mean: \(\E(y \mid x)\)
- Set up a prior predictive distribution \(f(y)\)
- After observing data \(y\), we treat \(f(y \mid \theta, x)\) as the likelihood of observing \(y\) under all plausible values of \(\theta\), conditioning on \(x\) if necessary
- Derive a posterior distribution for \(\theta\), \(\, f(\theta \mid y, x)\)
- Evaluate model quality: 1) quality of the inferences; 2) quality of predictions; go back to the beginning
- Compute derived quantities, such as \(\P(\theta > \alpha)\), \(f(\widetilde{y} \mid y)\), and \(d^* = \textrm{arg max}_d \ \E(U(z) \mid d)\)
For a more complete workflow, see Bayesian Workflow by Gelman et al. (2020)
Mystery Box Game Analysis
- Game Setup:
- You are offered to bet on the proportion of red balls in a box
- True proportions: \(\theta \in \{0.25,\, 0.50,\, 0.75\}\)
- You are allowed to draw 10 balls from the box with replacement
- Payoffs if your chosen \(\theta\) is correct:
- For \(\theta=0.25\): $3
- For \(\theta=0.50\): $5
- For \(\theta=0.75\): $15

- Your options are: A) Don’t play; B) Draw 10 balls, and pay $2 to play; C) Pay $1 to buy an extra ball (11th), then pay $2 to play
- Warmup: Before drawing 10 balls what is the expected value of each bet? Which one should we choose? (still have to pay $2 to play)
Example Prior Model
- What does it mean to put a uniform prior on \(\theta\)?
- What are we assuming about the game design under this prior?
- Is that a reasonable assumption, given the payoffs?
- We take one ball from the box; what is \(\P(y = \text{red})\)?
- Law of Total Probability (LOTP):
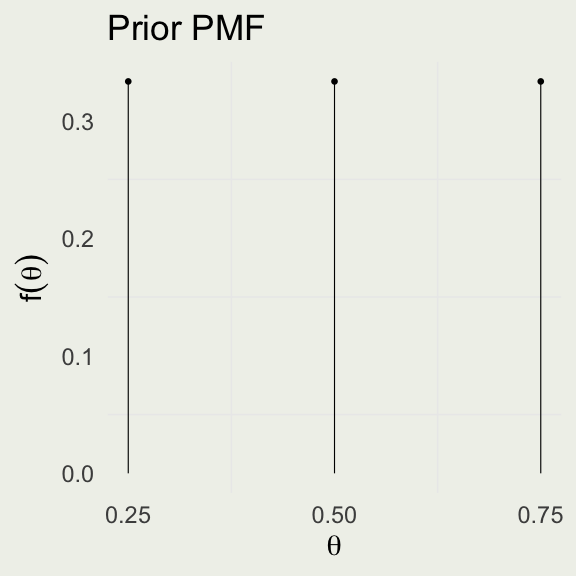
\[ \begin{eqnarray*} \P(y = \text{red}) &=& \sum_{i=1}^{3} f(y = \text{red}, \theta_i) = \sum_{i=1}^{3} f(y = \text{red} \mid \theta_i) f(\theta_i) \\ &=& (0.25) \cdot \left(\frac{1}{3}\right) + (0.50) \cdot \left(\frac{1}{3}\right) + (0.75) \cdot \left(\frac{1}{3}\right) \end{eqnarray*} \]
Data Model: Before Drawing 10 Balls
Take red ball as success, so \(y\) successes out of \(N = 10\) trials \[ y | \theta \sim \text{Bin}(N,\theta) = \text{Bin}(10,\theta) \]
\(f(y \mid \theta) = \text{Bin} (y \mid 10,\theta) = \binom{10}{y} \theta^y (1 - \theta)^{10 - y}\) for \(y \in \{0,1,\ldots,10\}\)
Is this a valid probability distribution as a function of \(y\)?

Visualizing the Likelihood Function
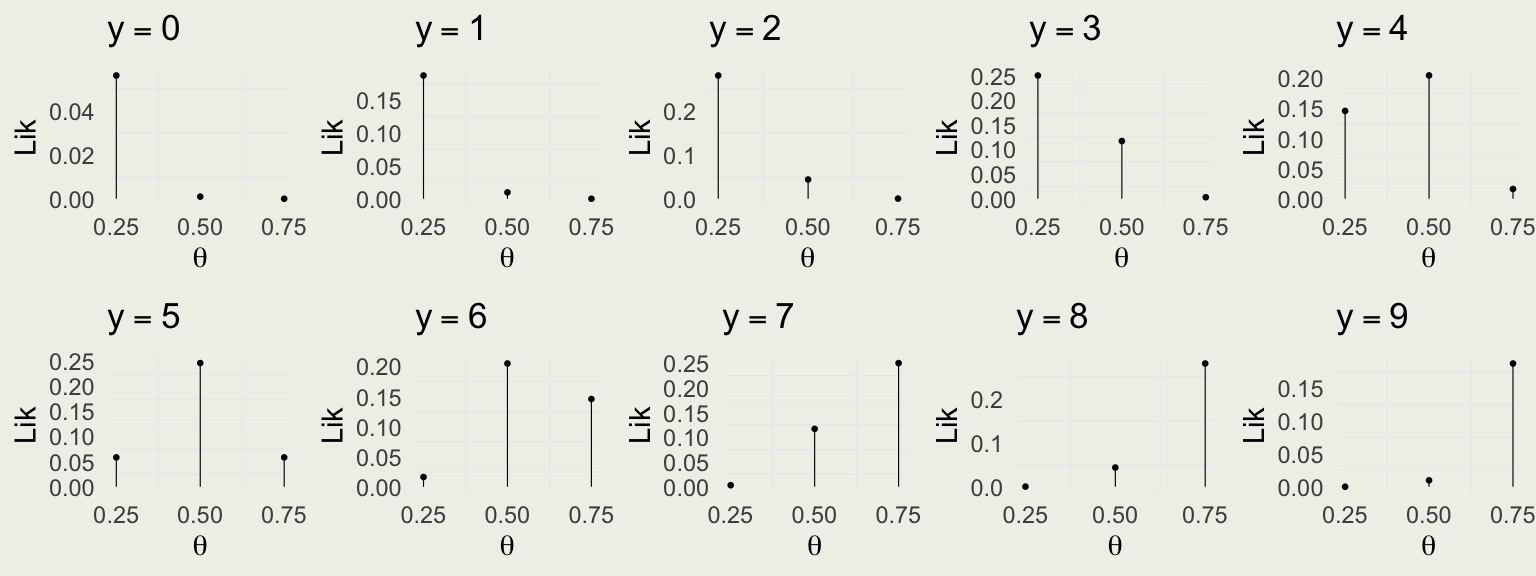
Compare with the data model:

Putting It All Together
- We observe 6 red balls, so we can condition on \(y = 6\)
- Let’s turn the Bayesian crank
\[ \begin{eqnarray*} f(\theta \mid y) &=& \frac{f(y \mid \theta) f(\theta)}{f(y)} = \frac{f(y \mid \theta) f(\theta)}{\sum_{i=1}^{3} f(y, \, \theta_i)} = \frac{f(y \mid \theta) f(\theta)}{\sum_{i=1}^{3} f(y \mid \theta_i) f(\theta_i)} \\ &\propto& f(y \mid \theta) f(\theta) \propto \theta^6 (1 - \theta)^{4} \end{eqnarray*} \]
- How many elements in \(f(\theta)\)?
- How many elements in \(f(\theta \mid y)\)?
Compute the Posterior
- We observed \(y = 6\), so \(f(y \mid \theta) \propto \theta^6 (1 - \theta)^{4}\)
- For \(\theta = 0.25\): (we can drop \(\binom{10}{6}\) term) \[ f(y | 0.25) = \binom{10}{6} (0.25)^6 (0.75)^4 \approx 0.02 \]
- For \(\theta = 0.50\): \[ f(y | 0.50) = \binom{10}{6} (0.5)^{10} \approx 0.21 \]
- For \(\theta = 0.75\): \[ f(y| 0.75 ) = \binom{10}{6} (0.75)^6 (0.25)^4 \approx 0.15 \]
| theta | prior | lik | lxp | post |
|---|---|---|---|---|
| 0.25 | 0.33 | 0.02 | 0.01 | 0.04 |
| 0.5 | 0.33 | 0.21 | 0.07 | 0.56 |
| 0.75 | 0.33 | 0.15 | 0.05 | 0.40 |
| Total | 1.00 | 0.37 | 0.12 | 1.00 |
Option 1: Play Immediately
- Let \(x_i\) represent the payoffs for each option \(i\)
- You want to choose \(\theta^*\), such that the utility is maximized; here we take it to be linear in the payoffs:
\[ \theta^* = \textrm{arg max}_{\theta} \left\{ x_i \times f(\theta_i \mid y) - \text{Cost} \right\} \]
- Bet on \(\theta=0.25\): \(3 \times 0.044 - 2 \approx -\$1.87\)
- Bet on \(\theta=0.50\): \(5 \times 0.559 - 2 \approx \$0.80\)
- Bet on \(\theta=0.75\): \(15 \times 0.397 - 2 \approx \$3.96\)
- We bet on \(\theta^*=0.75\) with expected payoff of $3.96, compared with $3 before we drew 10 balls
Warning
The bet on the most likely outcome, \(\theta=0.50\) (MLE), is suboptimal!
Option 2: Should You Buy an Extra Ball?
- We need to average over uncertainty of the red vs green ball
- Instead of \(f(\theta) = 1/3\), we use \(f(\theta \mid y)\), where y is 6 reds out of 10
- Compute the probability of red on the next draw (LOTP conditional on \(y\)):
\[ \begin{eqnarray*} \P(\tilde{y} = \text{red} \mid y) &=& \sum_{i=1}^{3} f(\tilde{y} = \text{red}, \ \theta_i \mid y) = \sum_{i=1}^{3} f(\tilde{y} = \text{red} \mid \theta_i, \ y) f(\theta_i \mid y) \\ &=& \sum_{i=1}^{3} f(\tilde{y} = \text{red} \mid \theta_i) f(\theta_i \mid y) \\ \P(\tilde{y} = \text{red} \mid y) &=& 0.25 \times 0.044 +0.5 \times 0.559 + 0.75 \times 0.397 \\ &\approx& 0.589 \end{eqnarray*} \]
- Posterior predictive probability of green: \(\P(\text{green}) = 1 - \P(\text{red}) \approx 0.411\)
Updating Beliefs With the Extra Ball
Case 1: Extra Ball is Red
- Update: Multiply the original posterior for each \(\theta\) by \(\theta\):
- For \(\theta=0.25\): \(0.044 \times 0.25 = 0.011\)
- For \(\theta=0.50\): \(0.559 \times 0.5 = 0.280\)
- For \(\theta=0.75\): \(0.397 \times 0.75 = 0.298\)
- Normalized probabilities:
- \(\P(0.25|\text{red}) \approx \frac{0.011}{0.589} \approx 0.019\)
- \(\P(0.50|\text{red}) \approx \frac{0.280}{0.589} \approx 0.475\)
- \(\P(0.75|\text{red}) \approx \frac{0.298}{0.589} \approx 0.506\)
- Expected prizes:
- Bet on \(\theta=0.25\): \(0.019 \times 3 \approx 0.057\)
- Bet on \(\theta=0.50\): \(0.475 \times 5 \approx 2.375\)
- Bet on \(\theta=0.75\): \(0.506 \times 15 \approx 7.593\)
Case 2: Extra Ball is Green
- Update: Multiply the original posterior by \((1-\theta)\):
- For \(\theta=0.25\): \(0.044 \times 0.75 = 0.033\)
- For \(\theta=0.50\): \(0.559 \times 0.5 = 0.280\)
- For \(\theta=0.75\): \(0.397 \times 0.25 = 0.099\)
- Normalized probabilities:
- \(\P(0.25|\text{green}) \approx \frac{0.033}{0.412} \approx 0.080\)
- \(\P(0.50|\text{green}) \approx \frac{0.280}{0.412} \approx 0.680\)
- \(\P(0.75|\text{green}) \approx \frac{0.099}{0.412} \approx 0.240\)
- Expected prizes:
- Bet on \(\theta=0.25\): \(0.080 \times 3 \approx 0.240\)
- Bet on \(\theta=0.50\): \(0.680 \times 5 \approx 3.400\)
- Bet on \(\theta=0.75\): \(0.240 \times 15 \approx 3.600\)
Overall Expected Prize With the Extra Ball
Combine the two cases:
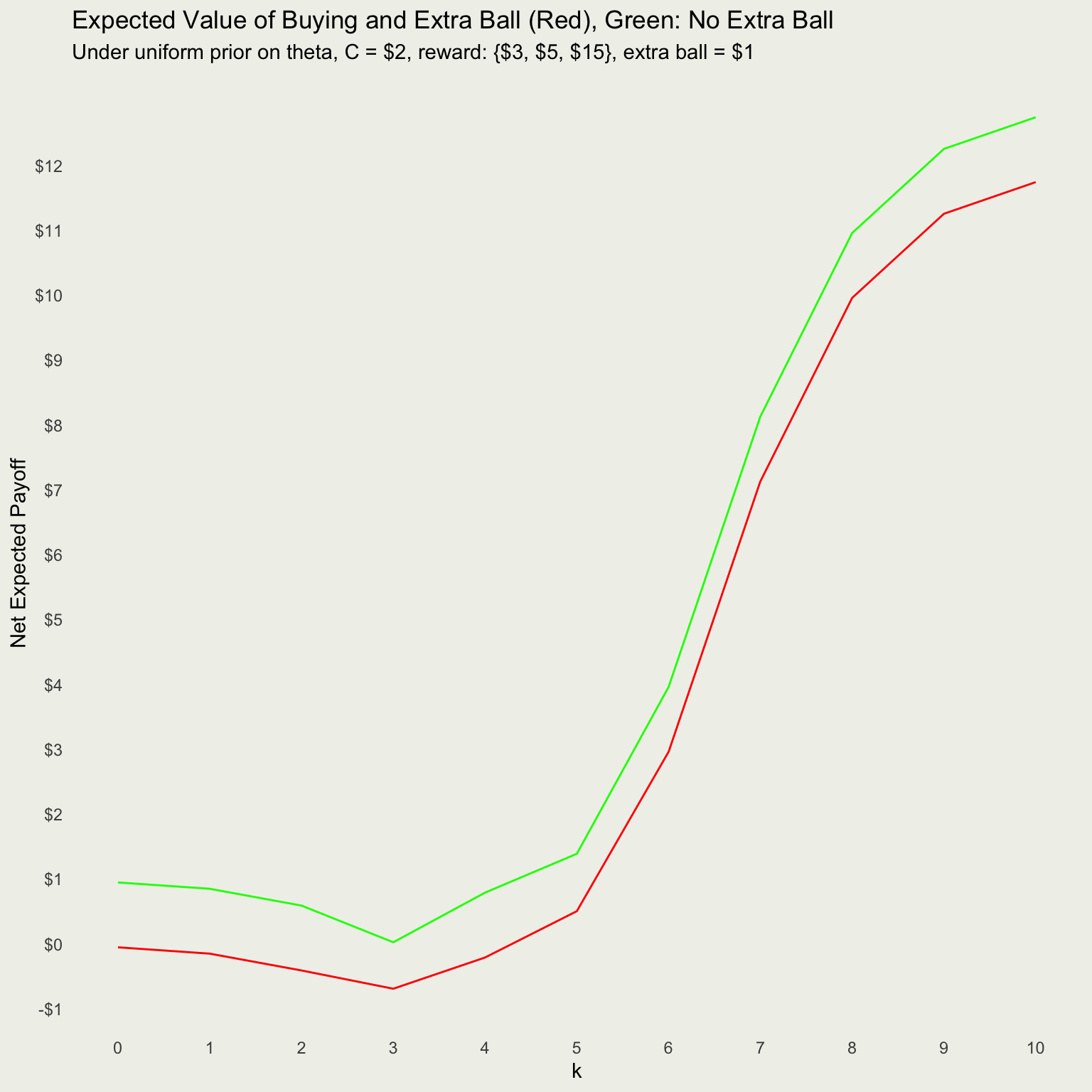
\[ \begin{align*} \E_\text{extra_ball}({\text{payoff}}) =& \P(\text{red})\times7.593 + \P(\text{green})\times3.600 \\ =& 0.589 \times 7.593 + 0.411 \times 3.600 \approx 5.95 \end{align*} \]
Net Expected Payoff (including costs):
- Extra ball cost: $1
- Play cost: $2
\[ \E_\text{extra_ball}({\text{payoff}}) = 5.95 - 3 = \$2.95. \]
Without the extra ball: Net EV \(\approx \$3.96\).
With the extra ball: Net EV \(\approx \$2.95\).
Decision: It is better to pay $2 and play immediately rather than buying an extra ball.
What About For All Possible Outcomes?
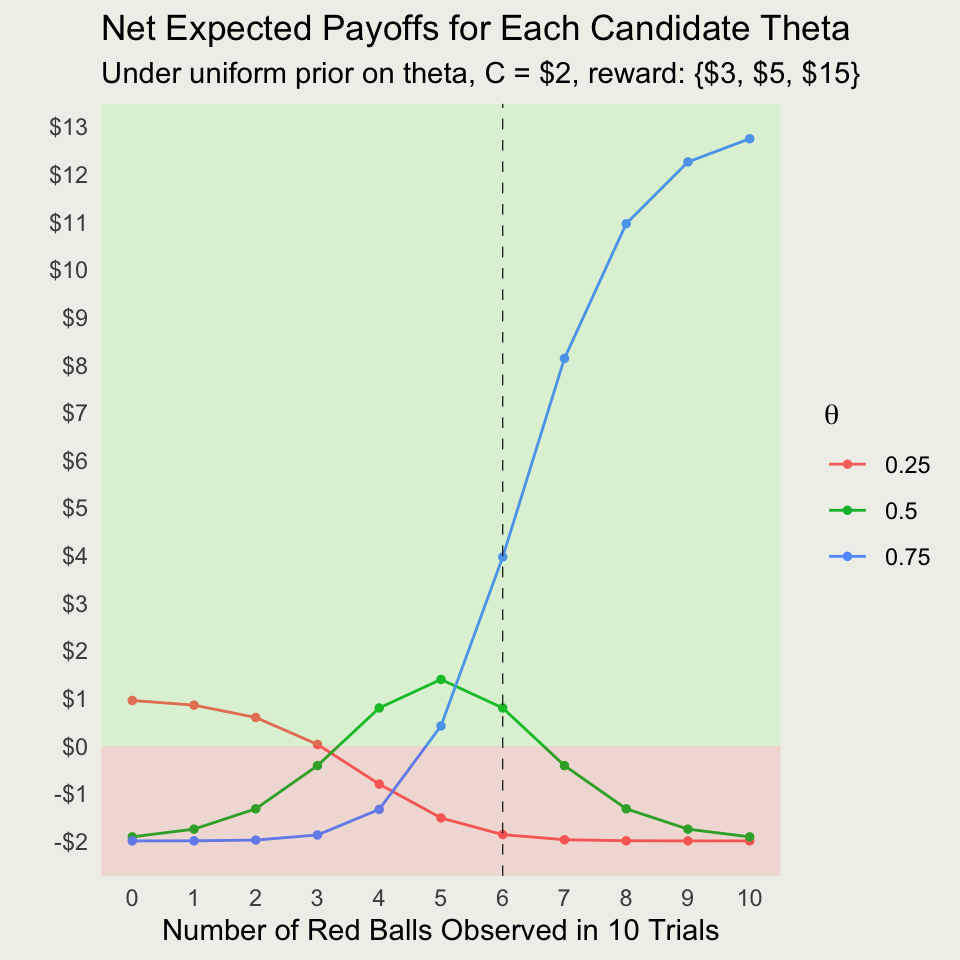
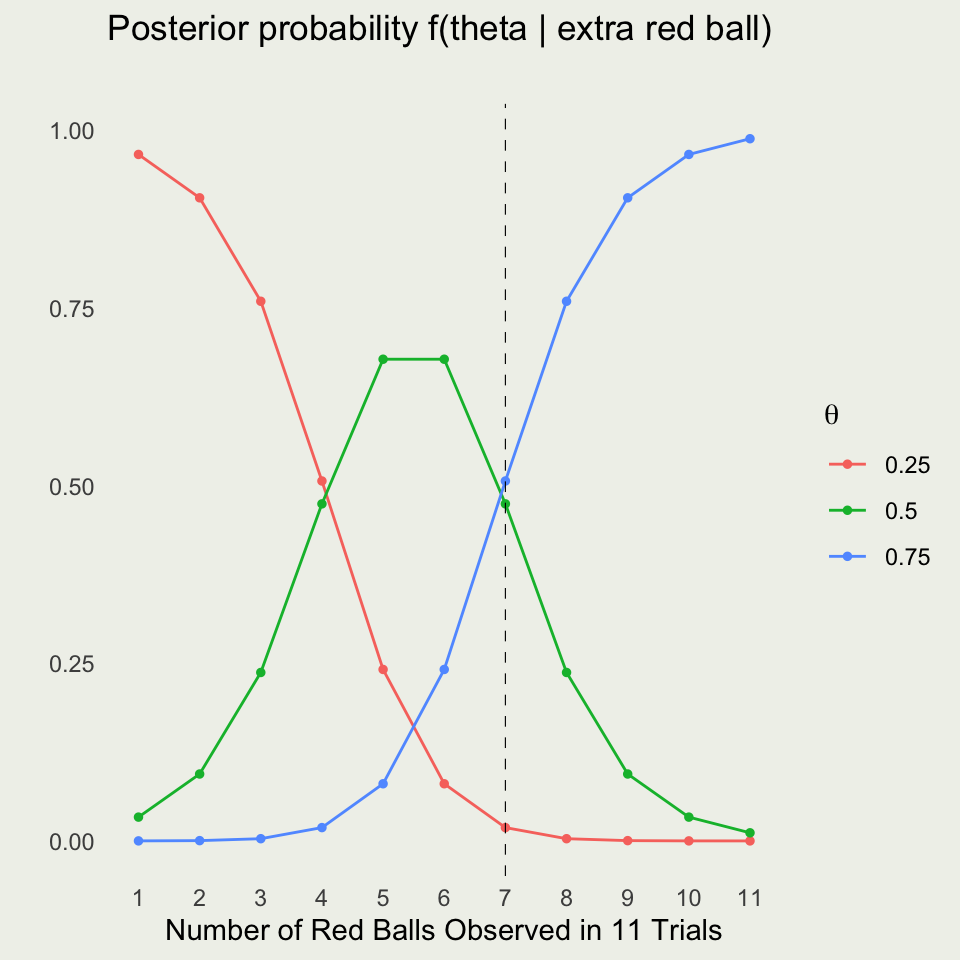
Net Payoffs With and Without Extra Ball?