Bayesian Inference

NYU Applied Statistics for Social Science Research

Eric Novik | Spring 2024 | Lecture 7

Logistic Regression and Introduction to Hierarchical Models

• GLMs and logistic regression
• Understanding logistic regression
• Simulating data
• Prior predictive simulations
• Example: Diabetes in Pima native americans
• Introducing hierarchical/multi-level models
• Pooling: none, complete, and partial
• Example hierarchical model

\[ \DeclareMathOperator{\E}{\mathbb{E}} \DeclareMathOperator{\P}{\mathbb{P}} \DeclareMathOperator{\V}{\mathbb{V}} \DeclareMathOperator{\L}{\mathcal{L}} \DeclareMathOperator{\I}{\text{I}} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \]

Logit and Inverse Logit

• In logistic regression, we have to map from probability space to the real line and from the real line back to probability
• Logistic function (log odds) achieves the former: \[ \text{logit}(p) = \log\left(\frac{p}{1-p}\right) \]
• Inverse logit achieves the latter: \[ \text{logit}^{-1}(x) = \frac{e^x}{1 + e^x} \]
• Notice that \(\text{logit}^{-1}(5)\) is very close to 1 and \(\text{logit}^{-1}(-5)\) is very close to 0
• In R, you can set logit <- qlogis and invlogit <- plogis

GLMs and Models For 0/1 Outcomes

• Modeling a probability of an event can be framed in the GLM context (just like with counts)
• The general setup is that we have:
  • Response vector \(y\) consisting of zeros and ones
  • The data model is \(y_i \sim \text{Bernoulli}(p_i)\)
  • Linear predictor: \(\eta_i = \alpha + X_i\beta\), where \(X\) is a matrix
  • In general: \(\E(y \mid X) = g^{-1}(\eta)\), where \(g^{-1}\)is the inverse link function that maps the linear predictor onto the observational scale
  • In particular: \(\E(y_i \mid X_i) = \text{logit}^{-1}(\alpha + X_i\beta) = p_i = \P(y_i = 1)\)
    • \(\text{logit}(p_i) = \eta_i\) and \(p_i = \text{logit}^{-1}(\eta_i)\)

Logistic Posterior

• To derive the posterior distribution for Poisson, we consider K regression inputs and independent priors on all \(K + 1\) unknowns: \(\alpha\) and \(\beta_1, \beta_2, ..., \beta_k\)

• Bernoulli likelihood is: \(f(y \mid p) = p^y (1 - p)^{1-y}\) with \(y \in \{0, 1\}\)

• And each \(p_i = \text{logit}^{-1}(\alpha + X_i\beta)\) \[ f\left(\alpha,\beta \mid y,X\right) \propto f_{\alpha}\left(\alpha\right) \cdot \prod_{k=1}^K f_{\beta}\left(\beta_k\right) \cdot \\ \prod_{i=1}^N \left(\text{logit}^{-1}(\alpha + X_i\beta) \right)^{y_i} \left(1 - \text{logit}^{-1}(\alpha + X_i\beta)\right)^{1-y_i} \]

• In Stan, the likelihood term can be written on a log scale as y ~ bernoulli_logit_glm(x, alpha, beta) or bernoulli_logit_glm_lupmf(y | x, alpha, beta)

Logistic Simulation

• As before, we can forward simulate data for logistic regression
• We will fit the data and try to recover the parameters

set.seed(123)
logit <- qlogis; invlogit <- plogis
n <- 100
a <- 1.2
b <- 0.4
x <- runif(n, -15, 10)
eta <- a + x * b
Pr <- invlogit(eta)
y <- rbinom(n, 1, Pr)
sim <- tibble(y, x, Pr)

p <- ggplot(aes(x, y), data = sim)
p <- p + geom_point(size = 0.5) +
  geom_line(aes(x, Pr), linewidth = 0.2) +
  geom_vline(xintercept = 0, color = "red", linewidth = 0.2, 
             linetype = "dashed", alpha = 1/3) +
  geom_hline(yintercept = invlogit(a), color = "red", linewidth = 0.2, 
             linetype = "dashed", alpha = 1/3) +
  geom_hline(yintercept = 0.50, linewidth = 0.2, linetype = "dashed", alpha = 1/3) +
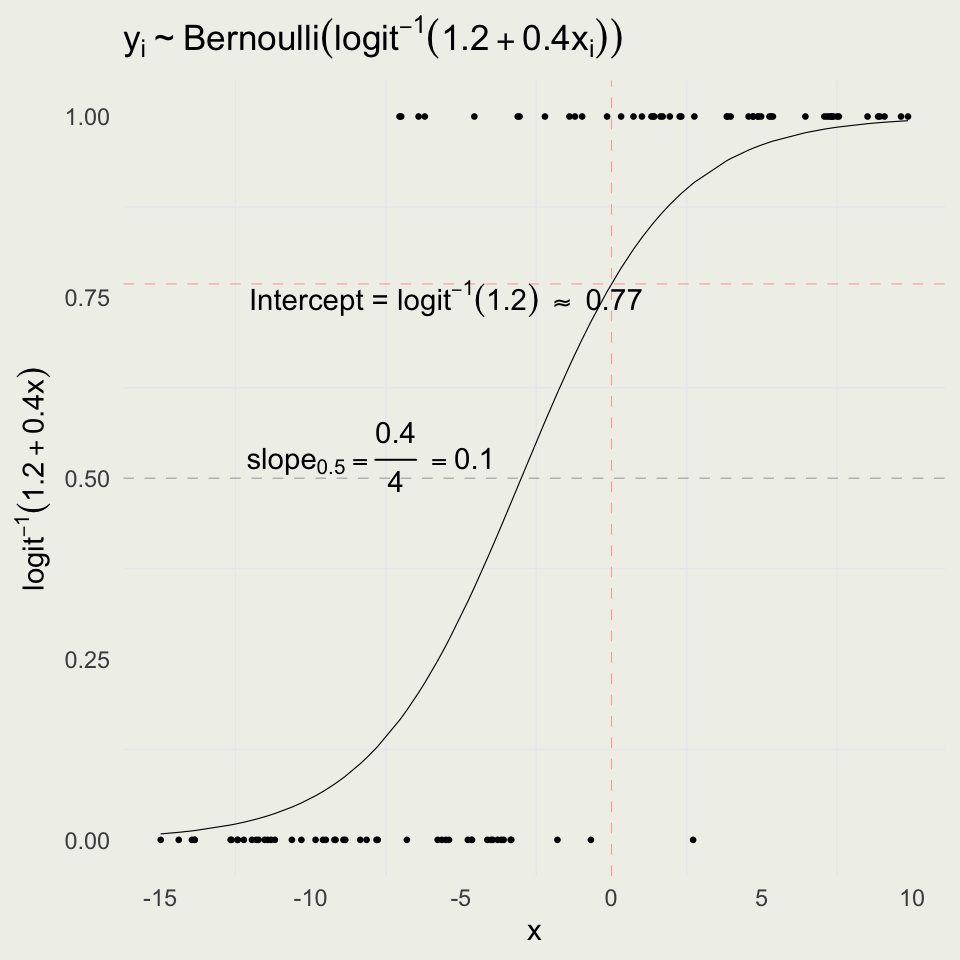
  ggtitle(TeX("$y_i \\sim Bernoulli(logit^{-1}(1.2 + 0.4x_i))$")) +
  annotate("text", x = -5.5, y = invlogit(a) - 0.02,
           label = TeX("Intercept = $logit^{-1}(1.2)$ \\approx 0.77")) +
  annotate("text", x = -8, y = 0.53,
           label = TeX("$slope_{.5} = \\frac{0.4}{4} = 0.10$")) +
  ylab(TeX("$logit^{-1}(1.2 + 0.4x)$")); print(p)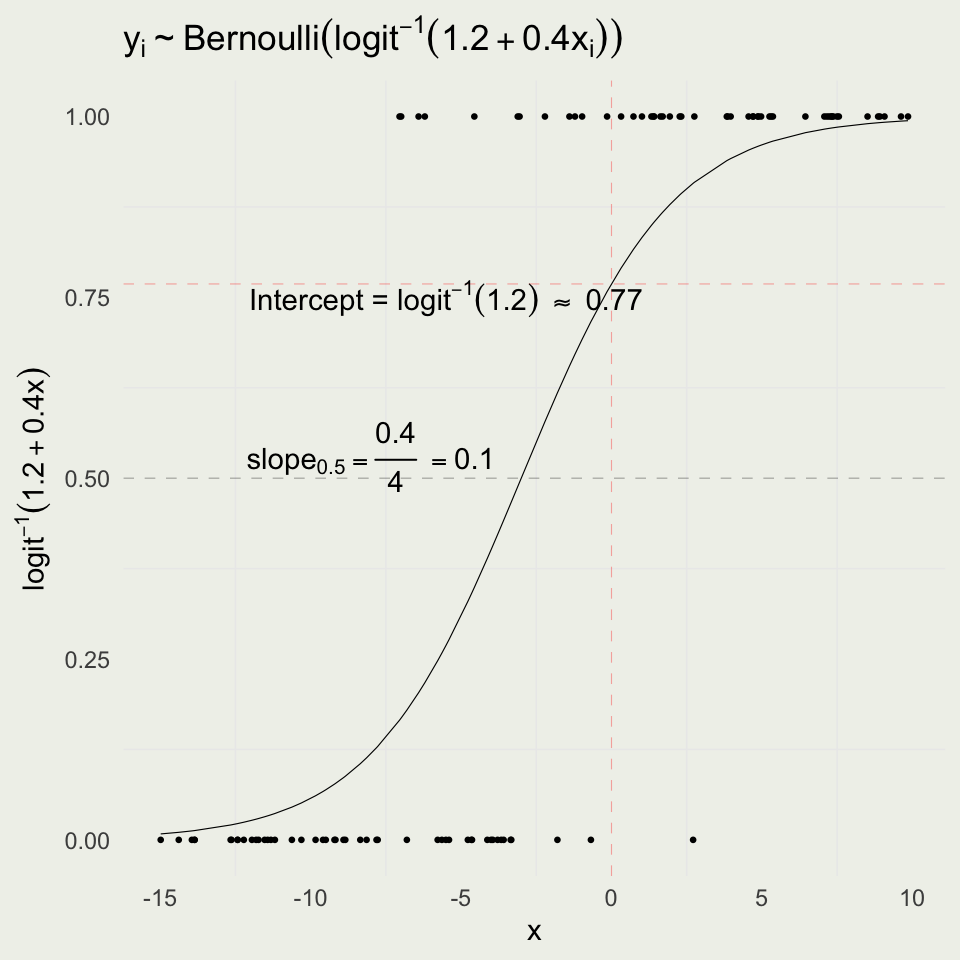

Interpreting Logistic Coefficients

• The intercept is the log odds of an event when \(x = 0\), \(\text{logit}^{-1}(1.2) = 0.77\)
• The slope changes depending on where you are on the curve
• When you are near 0.50, the slope of logit(x) is 1/4 and so you can divide your coefficient by 4 to get a rough estimate
• This implies that if we go from \(x = -3\) to \(x = -2\), the probability will increase by about 0.10

(invlogit(1.2 + 0.4 * -2) - 
   invlogit(1.2 + 0.4 * -3)) |> 
  round(2)

[1] 0.1

Fitting Simulated Data

• Complex and non-linear models may have a hard time recovering parameters from forward simulations
• The process for fitting simulated data may give some insight into the data-generating process and priors

# fitting from eta = 1.2 +  0.4 * x
m1 <- stan_glm(y ~ x,
               prior_intercept = normal(0, 1),
               prior = normal(0, 1),
               family = binomial(link = "logit"), 
               data = sim,
               chains = 4,
               refresh = 0,
               iter = 1000)
summary(m1)

Model Info:

 function:     stan_glm
 family:       binomial [logit]
 formula:      y ~ x
 algorithm:    sampling
 sample:       2000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 100
 predictors:   2

Estimates:
              mean   sd   10%   50%   90%
(Intercept) 1.5    0.5  0.9   1.5   2.1  
x           0.5    0.1  0.4   0.5   0.7  

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 0.5    0.0  0.5   0.5   0.6  

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.0  1.0  1132 
x             0.0  1.0  1106 
mean_PPD      0.0  1.0  1584 
log-posterior 0.0  1.0   817 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Generating Probability Data

• To get a sense of the variability in probability we can simulate from the prior distribution on the probability scale

prior_pred_logit <- function(x) {
  a <- rnorm(1, mean = 1.2, sd = 0.5)
  b <- rnorm(1, mean = 0.4, sd = 0.1)
  Pr <- invlogit(a + b * x)
  return(Pr)
}
prior_pred <- replicate(50, prior_pred_logit(x)) |>
  as.data.frame()

df_long <- prior_pred |>
  mutate(x = x) |>
  pivot_longer(cols = -x, names_to = "line", values_to = "y")

p <- ggplot(aes(x, y), data = df_long)
p + geom_line(aes(group = line), linewidth = 0.2, alpha = 1/5) +
  geom_line(aes(y = Pr), data = sim, linewidth = 0.5, color = 'red') +
  ylab(TeX("$logit^{-1}(\\alpha + \\beta x)$")) +
  ggtitle(TeX("Simulating from prior $logit^{-1}(\\alpha + \\beta x_i))$"),
  subtitle = TeX("$\\alpha \\sim Normal(1.2, 0.5)$ and $\\beta \\sim Normal(0.4, 0.1)$"))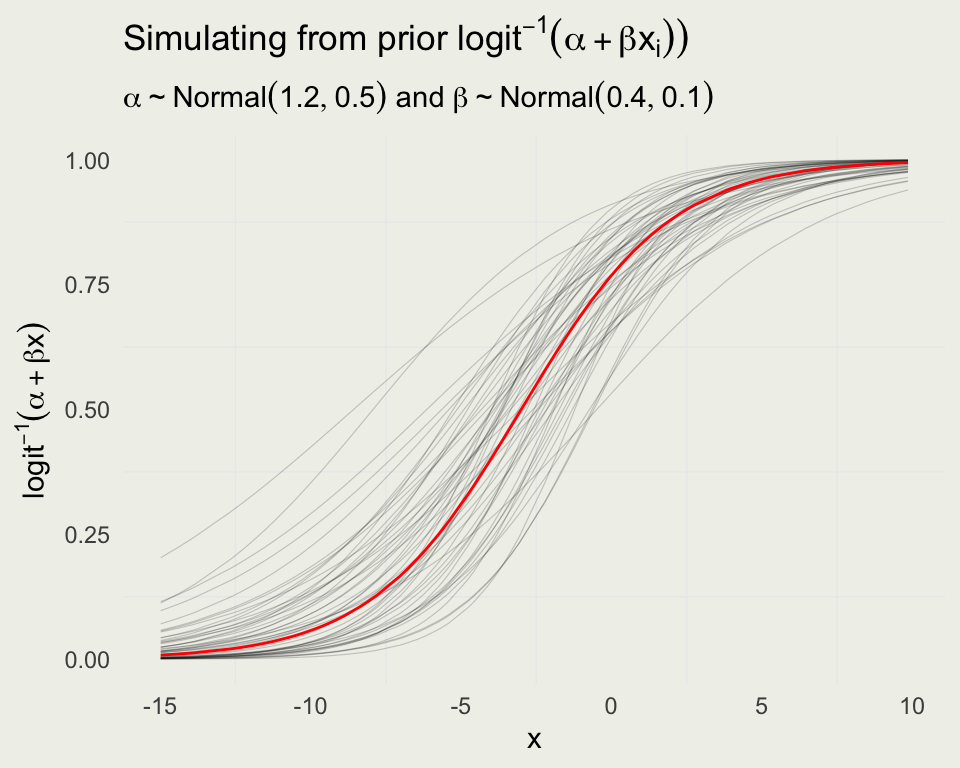 

Example: Diabetes

• This example comes from US National Institute of Diabetes and Digestive and Kidney Diseases from a population of women who were at least 21 years old, of Pima Indian heritage, and living near Phoenix, Arizona
• It is available as part of the R package pdp
• The outcome \(diabetes\), is an indicator of the disease
• Some other variables are:

pregnant	glucose	pressure	triceps	insulin	mass	pedigree	age	diabetes
6	148	72	35	NA	33.6	0.627	50	pos
1	85	66	29	NA	26.6	0.351	31	neg
8	183	64	NA	NA	23.3	0.672	32	pos
1	89	66	23	94	28.1	0.167	21	neg
0	137	40	35	168	43.1	2.288	33	pos
5	116	74	NA	NA	25.6	0.201	30	neg

Missing Value Imputation

• This dataset contains missing values
• People typically either delete them or replace them with average values, or something like that
• None of these are good approaches
• In R, we recommend a combination of the mice package and brms, which works nicely with mice
• From a Bayesian perspective, a missing value is just another unknown parameter in the model, which can be modeled

• Following is an example of a simple missing value estimation from the Stan manual

data {
  int<lower=0> N_obs;
  int<lower=0> N_mis;
  array[N_obs] real y_obs;
}
parameters {
  real mu;
  real<lower=0> sigma;
  array[N_mis] real y_mis;
}
model {
  y_obs ~ normal(mu, sigma);
  y_mis ~ normal(mu, sigma);
}

• Notice, that you need to make an assumption about the model for missing values

Example: Diabetes

• Code
• Plot

• It is well-known that people with high BMI are at risk for Type 2 diabetes
• We can do some exploratory analysis to check this

p1 <- ggplot(pima, aes(x = mass)) + 
  geom_density(aes(group = diabetes, fill = diabetes, color = diabetes), alpha = 1/5) +
  xlab("BMI")
p2 <- pima |>
  drop_na() |>
  mutate(bmi_cut = cut(mass, breaks = seq(15, 70, by = 5))) |>
  group_by(bmi_cut) |>
  summarize(p = mean(diabetes == "pos"),
            n = n(),
            se = sqrt(p * (1 - p) / n),
            lower = p + se,
            upper = p - se) |>
  ggplot(aes(x = bmi_cut, y = p)) + 
  geom_point() + geom_linerange(aes(ymin = lower, ymax = upper), linewidth = 0.2) +
  xlab("BMI range") + ylab("Proportion") +
  ggtitle("Proportion of diabetics by BMI +/- 1 SE")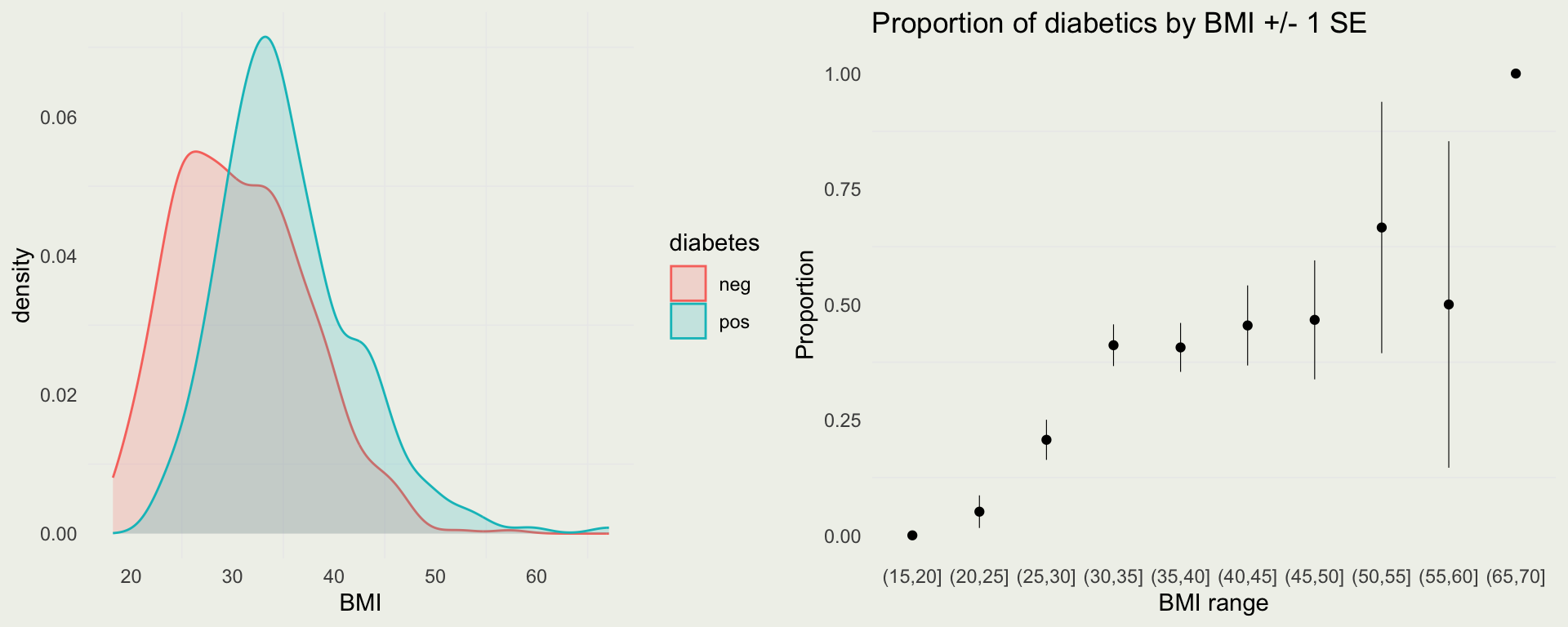

Example: Diabetes

• Before building a model, we should scale the variables

library(pdp)
d <- pima |>
  as_tibble() |>
  select(diabetes, age, pedigree, mass, glucose) |>
  drop_na() |> # in an important analysis, you should not do this; instead, impute
  mutate(diab = if_else(diabetes == "pos", 1, 0),
         age = (age - mean(age)) / 10,
         pedigree = (pedigree - mean(pedigree)),
         bmi = ((mass - mean(mass)) / 10),
         glucose = ((glucose - mean(glucose)) / sd(glucose))) 
head(d)

# A tibble: 6 × 7
  diabetes     age pedigree  mass glucose  diab    bmi
  <fct>      <dbl>    <dbl> <dbl>   <dbl> <dbl>  <dbl>
1 pos       1.67      0.154  33.6   0.852     1  0.115
2 neg      -0.231    -0.122  26.6  -1.21      0 -0.585
3 pos      -0.131     0.199  23.3   2.00      1 -0.915
4 neg      -1.23     -0.306  28.1  -1.08      0 -0.435
5 pos      -0.0312    1.81   43.1   0.492     1  1.06 
6 neg      -0.331    -0.272  25.6  -0.194     0 -0.685

Example: Diabetes

• We will be fitting the following statistical model, where \(x\) is the BMI and \(\bar x\) is the average BMI in the sample
• We divide by ten so that a unit increase in BMI is a meaningful change
• We need to pick priors on \(\alpha\), and \(\beta\)

\[ \begin{eqnarray} y_i &\sim& \text{Bernoulli}(p_i) \\ \eta_i &=& \alpha + \beta \left( \frac{x_{i} - \bar x}{10} \right) \\ p_i &=& \frac{e^{\eta_i}}{1 + e^{\eta_i}} \\ \alpha &\sim& \text{Normal}(\mu_\alpha ,\ \sigma_\alpha) \\ \beta &\sim& \text{Normal}(\mu_\beta , \ \sigma_\beta) \end{eqnarray} \]

Example: Diabetes

• The prior on the intercept corresponds to the log odds of developing diabetes when a person has an average BMI, which is about 29 in the US (which is considered high-risk)
• It is likely that the probability is between 20% and 80%, and so a weakly informative prior can be expressed as \(\text{Normal}(0, 0.5)\), since invlogit(c(-1.5, 1.5)) = [0.18, 0.82]
• Suppose, we also put a weakly informative \(\text{Normal}(0, 1)\) pior on \(\beta\)

\[ \begin{eqnarray} y_i &\sim& \text{Bernoulli}(p_i) \\ \eta_i &=& \alpha + \beta \left( \frac{x_{i} - \bar x}{10} \right) \\ p_i &=& \frac{e^{\eta_i}}{1 + e^{\eta_i}} \\ \alpha &\sim& \text{Normal}(0 ,\ 0.5) \\ \beta &\sim& \text{Normal}(0 , \ 1) \end{eqnarray} \]

Example: Diabetes

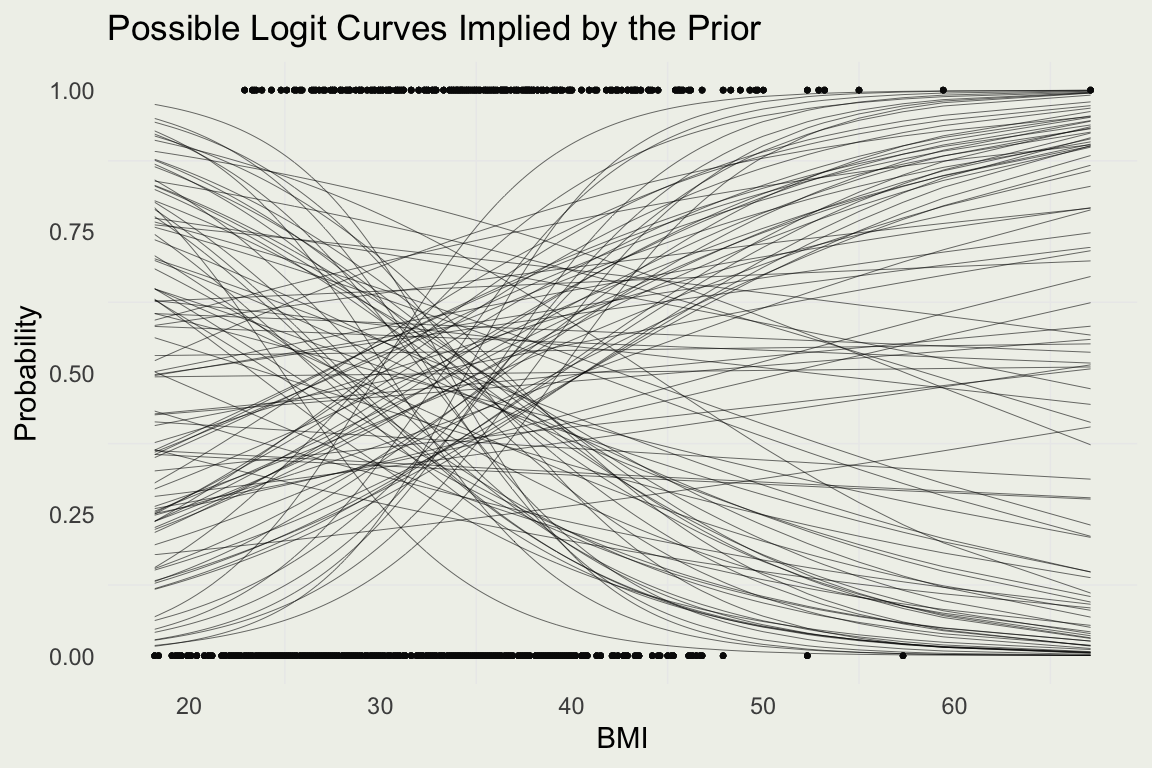
• Let’s perform prior predictive simulation

m_prior <- stan_glm(diab ~ bmi,
               prior_intercept = normal(0, 0.5),
               prior = normal(0, 1), 
               family = binomial(link = "logit"), 
               refresh = 100,
               prior_PD = TRUE,
               data = d, 
               refresh = 0,
               seed = 123,
               iter = 1000)

summary(m_prior)

Model Info:

 function:     stan_glm
 family:       binomial [logit]
 formula:      diab ~ bmi
 algorithm:    sampling
 sample:       2000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 752
 predictors:   2

Estimates:
              mean   sd   10%   50%   90%
(Intercept)  0.0    0.5 -0.6   0.0   0.6 
bmi          0.0    1.0 -1.3   0.0   1.3 

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.0  1.0  1215 
bmi           0.0  1.0  1108 
log-posterior 0.0  1.0   932 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Example: Diabetes

d |>
  add_epred_draws(m_prior, ndraws = 100) |>
  ggplot(aes(x = mass, y = diab)) +
  geom_line(aes(y = .epred, group = .draw), size = 0.1) +
  geom_point(aes(mass, diab), alpha = 1/20, size = 0.5) +
  xlab("BMI") + ylab("Probability") +
  ggtitle("Possible Logit Curves Implied by the Prior")

Example: Diabetes

• The negative associations are implausible given everything we know about diabetes
• Suppose the risk of diabetes doubles for every 10 \(kg/m^2\) (unverified)
• That would imply average \(\beta \approx 0.7\), since the multiplicative change in odds is \(e^{0.7} \approx 2\)
• We will set the standard deviation to 0.2 to avoid negative effects and allow the odds to be as high as 3.5

\[ \begin{eqnarray} y_i &\sim& \text{Bernoulli}(p_i) \\ \eta_i &=& \alpha + \beta_1 \left( \frac{x_{i} - \bar x}{10} \right) \\ p_i &=& \frac{e^{\eta_i}}{1 + e^{\eta_i}} \\ \alpha &\sim& \text{Normal}(0 ,\ 0.5) \\ \beta &\sim& \text{Normal}(0.7 , \ 0.2) \end{eqnarray} \]

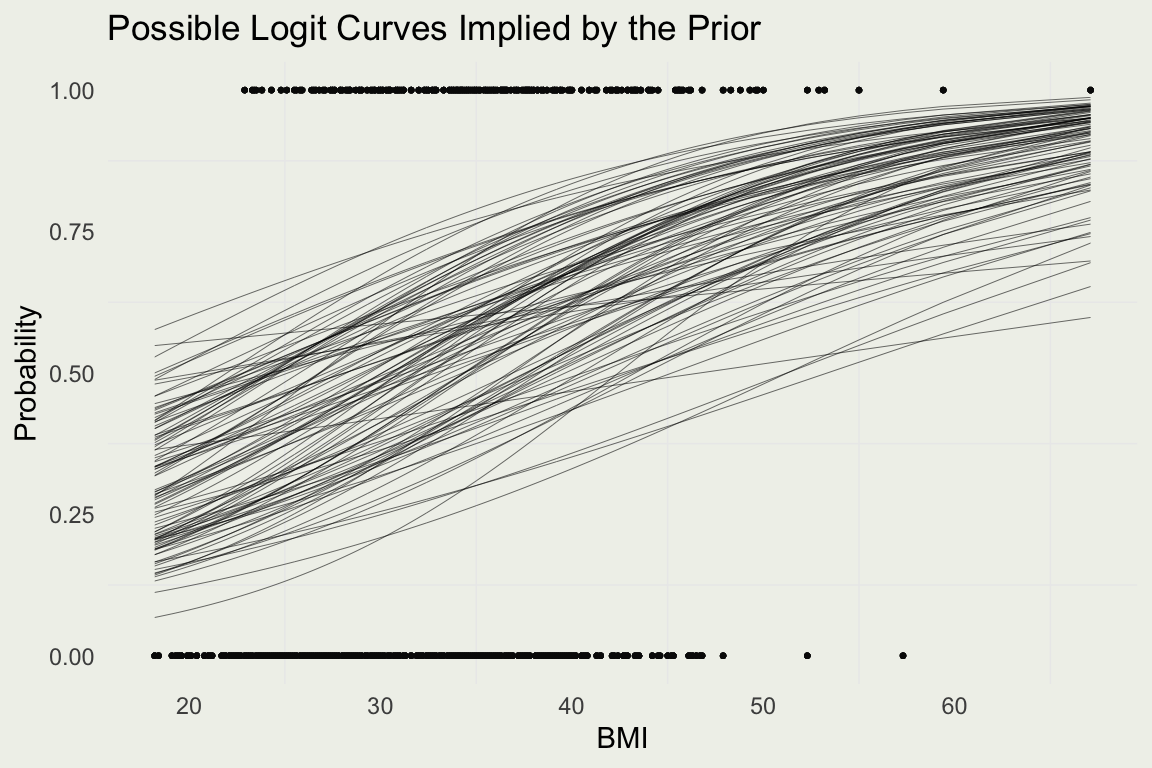
Example: Diabetes

• With new priors, let’s repeat the prior predictive simulation

m_prior <- stan_glm(diab ~ bmi,
               prior_intercept = normal(0, 0.5),
               prior = normal(0.7, 0.2), 
               family = binomial(link = "logit"), 
               refresh = 100,
               prior_PD = TRUE,
               data = d, 
               refresh = 0,
               seed = 123,
               iter = 1000)
summary(m_prior)

Model Info:

 function:     stan_glm
 family:       binomial [logit]
 formula:      diab ~ bmi
 algorithm:    sampling
 sample:       2000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 752
 predictors:   2

Estimates:
              mean   sd   10%   50%   90%
(Intercept)  0.0    0.5 -0.6   0.0   0.6 
bmi          0.7    0.2  0.4   0.7   1.0 

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.0  1.0  1215 
bmi           0.0  1.0  1108 
log-posterior 0.0  1.0   932 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Example: Diabetes

d |>
  add_epred_draws(m_prior, ndraws = 100) |>
  ggplot(aes(x = mass, y = diab)) +
  geom_line(aes(y = .epred, group = .draw), size = 0.1) +
  geom_point(aes(mass, diab), alpha = 1/20, size = 0.5) +
  xlab("BMI") + ylab("Probability") +
  ggtitle("Possible Logit Curves Implied by the Prior")

Example: Diabetes

• With this new prior we are ready to fit the model

m2 <- stan_glm(diab ~ bmi,
               prior_intercept = normal(0, 0.5),
               prior = normal(0.7, 0.2), 
               family = binomial(link = "logit"), 
               prior_PD = FALSE,
               data = d, 
               refresh = 0,
               seed = 123,
               iter = 1000)
summary(m2)

Model Info:

 function:     stan_glm
 family:       binomial [logit]
 formula:      diab ~ bmi
 algorithm:    sampling
 sample:       2000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 752
 predictors:   2

Estimates:
              mean   sd   10%   50%   90%
(Intercept) -0.6    0.1 -0.7  -0.6  -0.5 
bmi          0.9    0.1  0.8   0.9   1.1 

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 0.4    0.0  0.3   0.4   0.4  

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.0  1.0  1315 
bmi           0.0  1.0  1299 
mean_PPD      0.0  1.0  1651 
log-posterior 0.0  1.0   780 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Example: Diabetes

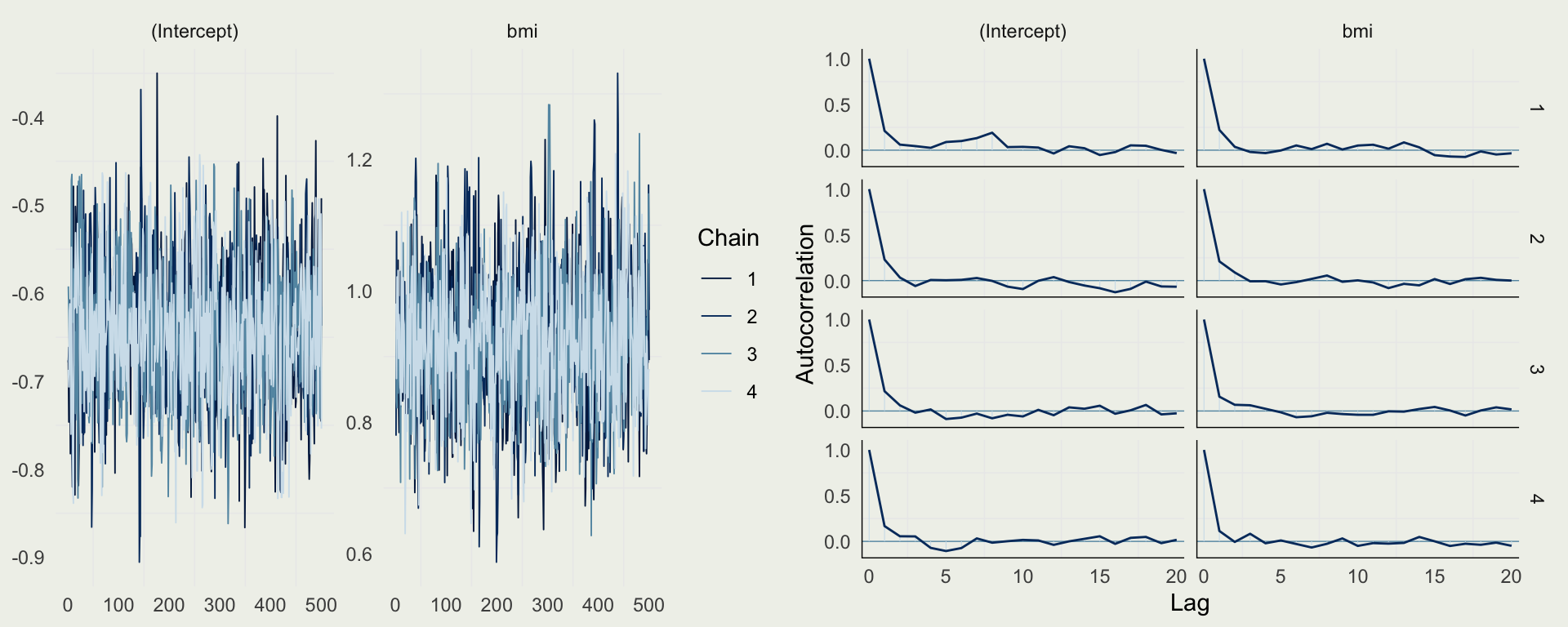
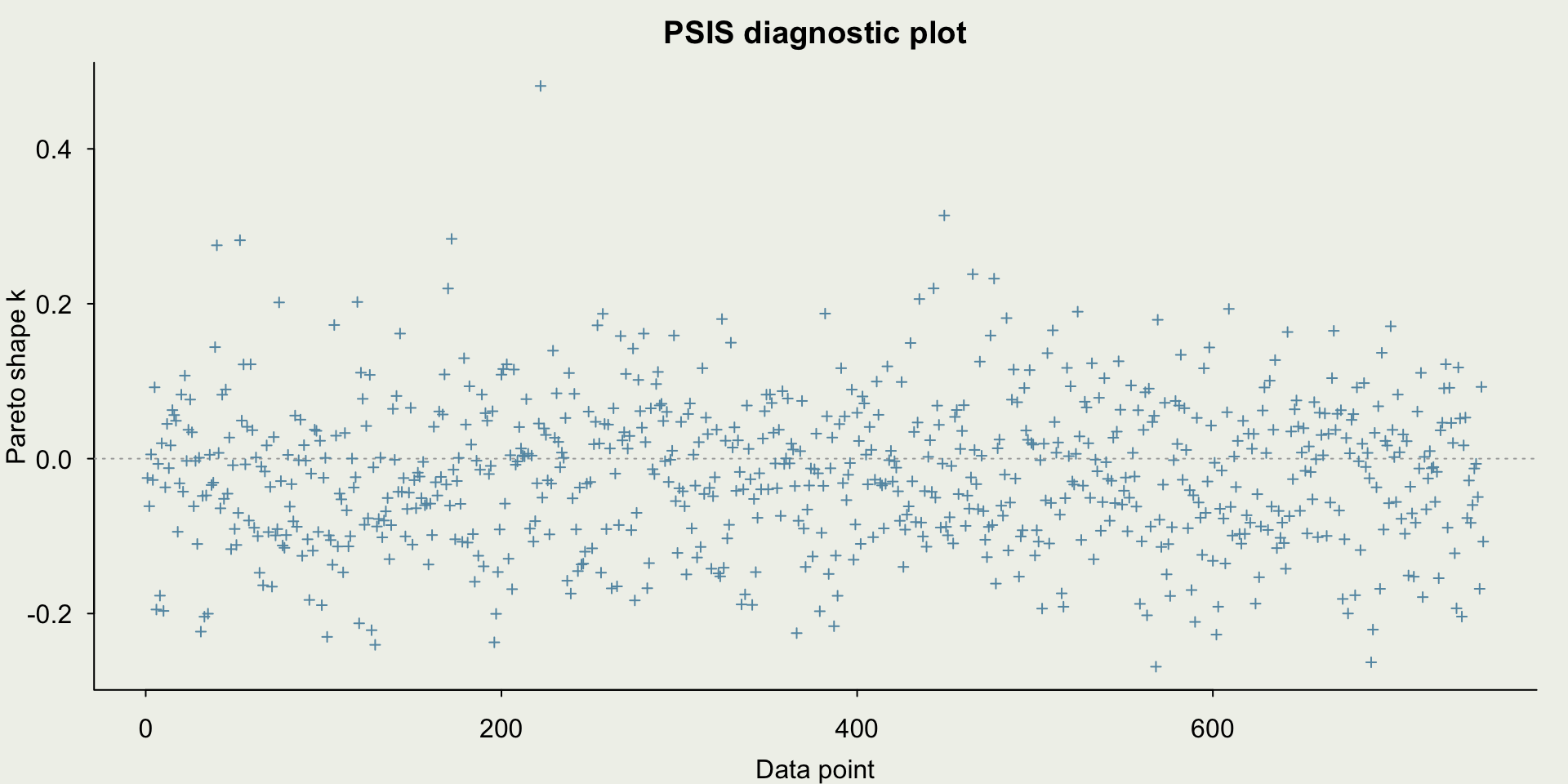
• There are no sampling problems, but we should still check the diagnostics

library(bayesplot)
p1 <- mcmc_trace(m2)
p2 <- mcmc_acf(m2)
grid.arrange(p1, p2, ncol = 2)

Example: Diabetes

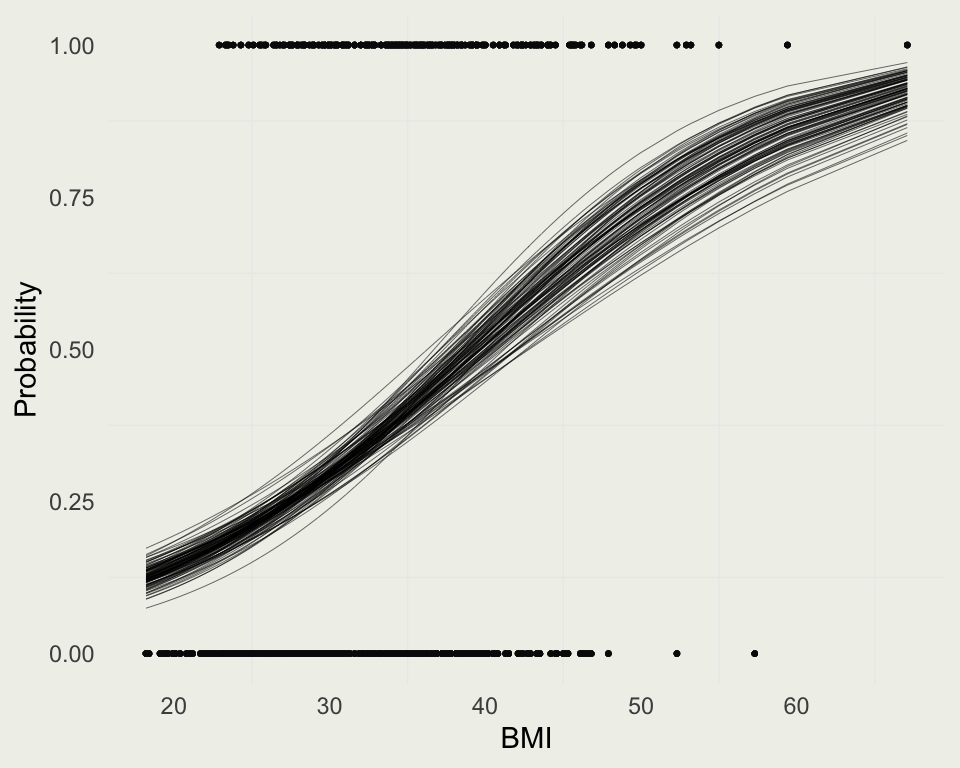
• We can examine the posterior probability of diabetes among this population (women who were at least 21 years old, and of Pima Indian heritage)

d |>
  add_epred_draws(m2, ndraws = 100) |>
  ggplot(aes(x = mass, y = diab)) +
  geom_line(aes(y = .epred, group = .draw), size = 0.1) +
  geom_point(aes(mass, diab), alpha = 1/20, size = 0.5) +
  xlab("BMI") + ylab("Probability")

Example: Diabetes

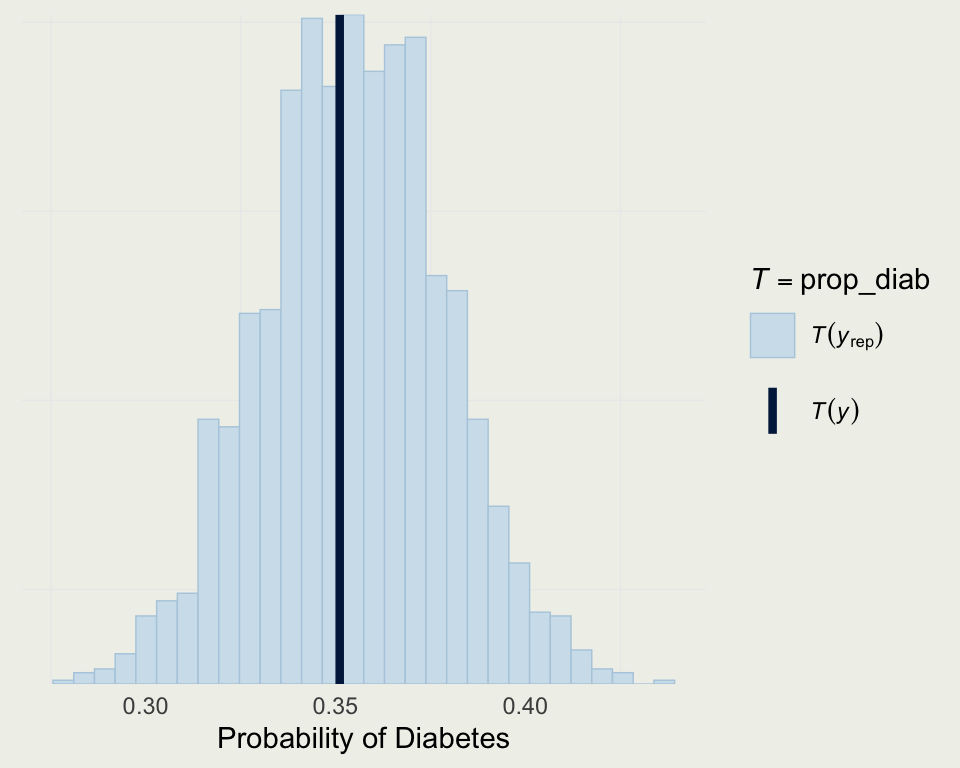
• We can also see the posterior predictive distribution of the probability of diabetes

prop_diab <- function(x) {
  mean(x == 1)
}
pp_check(m2, nreps = 100,
         plotfun = "stat", stat = "prop_diab") + xlab("Probability of Diabetes")

Example: Diabetes

• As before, we can compute predictions for new data using posterior_predict or by constructing the posterior distribution directly
• Let’s say we want to predict the probability of diabetes for a person with BMI = 40

bmi_scaled <- (40 - mean(d$mass)) / 10
yepred_m2 <- posterior_epred(m2, newdata = data.frame(bmi = bmi_scaled))
quantile(yepred_m2, probs = c(0.05, 0.50, 0.95)) |> round(2)

  5%  50%  95% 
0.47 0.51 0.56 

d_m2 <- as_tibble(m2) |>
  mutate(log_odds = `(Intercept)` + bmi * bmi_scaled,
         prob = invlogit(log_odds),
         ypred = rbinom(2e3, size = 1, prob = prob))
d_m2[1:3, ]

# A tibble: 3 × 5
  `(Intercept)`   bmi  log_odds  prob ypred
          <dbl> <dbl>     <dbl> <dbl> <int>
1        -0.676 0.897  0.000969 0.500     1
2        -0.746 0.936 -0.0403   0.490     0
3        -0.682 0.957  0.0402   0.510     0

quantile(d_m2$prob, probs = c(0.05, 0.50, 0.95)) |> round(2)

  5%  50%  95% 
0.47 0.51 0.56 

Example: Diabetes

• We will extend this model and evaluate the model performance
• Here we set weakly informative priors on the other three coefficients

priors <- normal(location = c(0.7, 0, 0, 0), 
                 scale = c(0.2, 1, 1, 1))
m3 <- stan_glm(diab ~ bmi + pedigree + 
                 age + glucose,
               prior_intercept = normal(0, 0.5),
               prior = priors,
               family = binomial(link = "logit"), 
               data = d, 
               refresh = 0,
               seed = 123,
               iter = 1000)
summary(m3)

Model Info:

 function:     stan_glm
 family:       binomial [logit]
 formula:      diab ~ bmi + pedigree + age + glucose
 algorithm:    sampling
 sample:       2000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 752
 predictors:   5

Estimates:
              mean   sd   10%   50%   90%
(Intercept) -0.8    0.1 -0.9  -0.8  -0.7 
bmi          0.8    0.1  0.7   0.8   1.0 
pedigree     0.8    0.3  0.5   0.8   1.2 
age          0.3    0.1  0.2   0.3   0.4 
glucose      1.1    0.1  0.9   1.1   1.2 

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 0.4    0.0  0.3   0.4   0.4  

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.0  1.0  2663 
bmi           0.0  1.0  2623 
pedigree      0.0  1.0  2128 
age           0.0  1.0  2551 
glucose       0.0  1.0  2861 
mean_PPD      0.0  1.0  2566 
log-posterior 0.1  1.0   747 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

ShinyStan Demo

• To use install.packages("shinystan") and launch_shinystan(m3)

Making Additional Improvements

• There is a good reason to believe that glucose and heredity interact so we will include an interaction term
• Age effects are rarely linear and so we include a B-Spline for non-linear age effects

library(splines)
priors <- normal(location = c(0.7, rep(0, 7)), 
                 scale = c(0.2, rep(1, 7)))
m4 <- stan_glm(diab ~ bmi + pedigree + 
                 bs(age, df = 4) + 
                 glucose + glucose:pedigree,
               prior_intercept = normal(0, 0.5),
               prior = priors,
               family = binomial(link = "logit"), 
               data = d, 
               refresh = 0,
               seed = 123,
               iter = 1000)
summary(m4)

Model Info:

 function:     stan_glm
 family:       binomial [logit]
 formula:      diab ~ bmi + pedigree + bs(age, df = 4) + glucose + glucose:pedigree
 algorithm:    sampling
 sample:       2000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 752
 predictors:   9

Estimates:
                   mean   sd   10%   50%   90%
(Intercept)      -1.6    0.3 -2.0  -1.6  -1.2 
bmi               0.8    0.1  0.6   0.8   0.9 
pedigree          0.9    0.3  0.6   0.9   1.3 
bs(age, df = 4)1  0.3    0.4 -0.2   0.3   0.8 
bs(age, df = 4)2  2.6    0.6  1.9   2.6   3.3 
bs(age, df = 4)3  0.7    0.7 -0.2   0.7   1.6 
bs(age, df = 4)4 -0.6    0.8 -1.6  -0.6   0.4 
glucose           1.1    0.1  1.0   1.1   1.3 
pedigree:glucose -0.6    0.3 -0.9  -0.6  -0.3 

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 0.4    0.0  0.3   0.4   0.4  

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
                 mcse Rhat n_eff
(Intercept)      0.0  1.0  1643 
bmi              0.0  1.0  2228 
pedigree         0.0  1.0  2015 
bs(age, df = 4)1 0.0  1.0  1758 
bs(age, df = 4)2 0.0  1.0  1999 
bs(age, df = 4)3 0.0  1.0  1853 
bs(age, df = 4)4 0.0  1.0  2086 
glucose          0.0  1.0  1749 
pedigree:glucose 0.0  1.0  1633 
mean_PPD         0.0  1.0  1912 
log-posterior    0.1  1.0   960 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Example: Diabetes

• We can perform model comparison using several methods
• One way is to assess classification accuracy under different probability cut points, which is often done in Machine Learning (ROC/AUC)
• A better way is to use LOO (loo and loo_compare in R)

par(mar = c(3,3,2,1), 
    mgp = c(2,.7,0), 
    tck = -.01, 
    bg  = "#f0f1eb")
m2_loo <- loo(m2)
m3_loo <- loo(m3)
m4_loo <- loo(m4)
loo_compare(m2_loo, m3_loo, m4_loo)

   elpd_diff se_diff
m4    0.0       0.0 
m3  -15.6       4.6 
m2 -104.5      12.4 

plot(m4_loo)

Introduction to Hierarchical Models

• You can think about hierarchical (sometimes called multi-level or mixed effects) models from a data or parameter perspective, although the parameter view is more fundamental
• The basic idea is that want to model all sources of potential variability in the data
• Data often arrive in clusters, such as students within schools, patients with hospitals, voters within states, and so on
• Since there are local influences, it is often a good idea to assume that units share similar attributes within clusters as well as between clusters
• These two sources of variability are likely different and we should treat them as such

Sleep Data

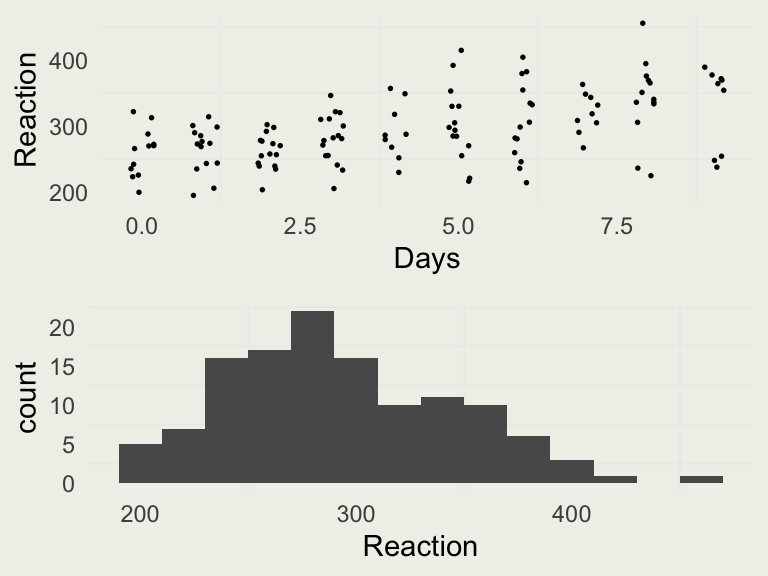
• Let’s look at a classic dataset called sleepstudy from lme4 package
• These data are from the study described in Belenky et al. (2003), for the most sleep-deprived group (3 hours time-in-bed) and for the first 10 days of the study, up to the recovery period

p <- ggplot(aes(Days, Reaction), data = lme4::sleepstudy)
p + geom_point(size = 0.3) + geom_line(linewidth = 0.1) + facet_wrap(vars(Subject)) + ylab("Reaction time (ms)")

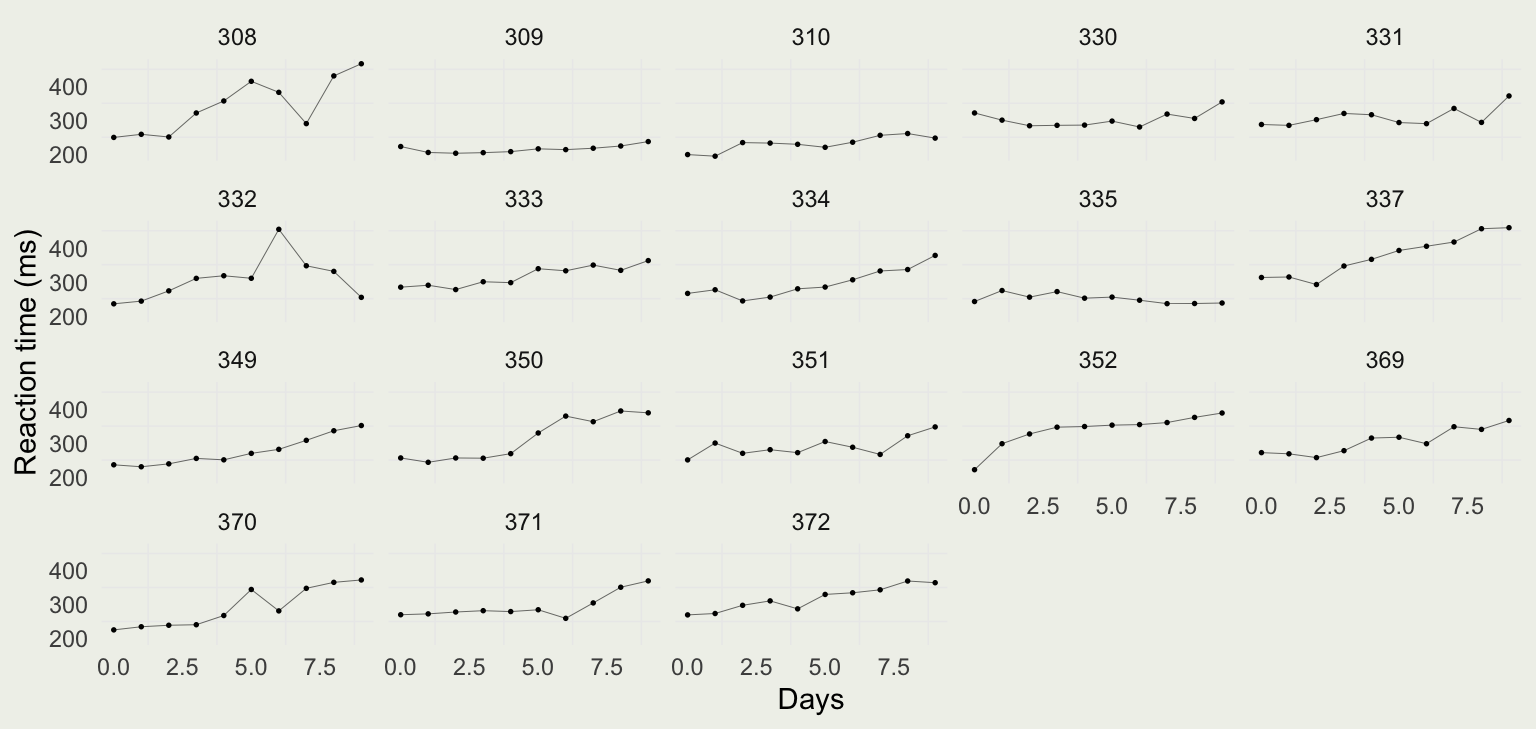
Sleep Data

• To get a better sense of the differences in per-Subject reaction time distributions, we can plot them side by side

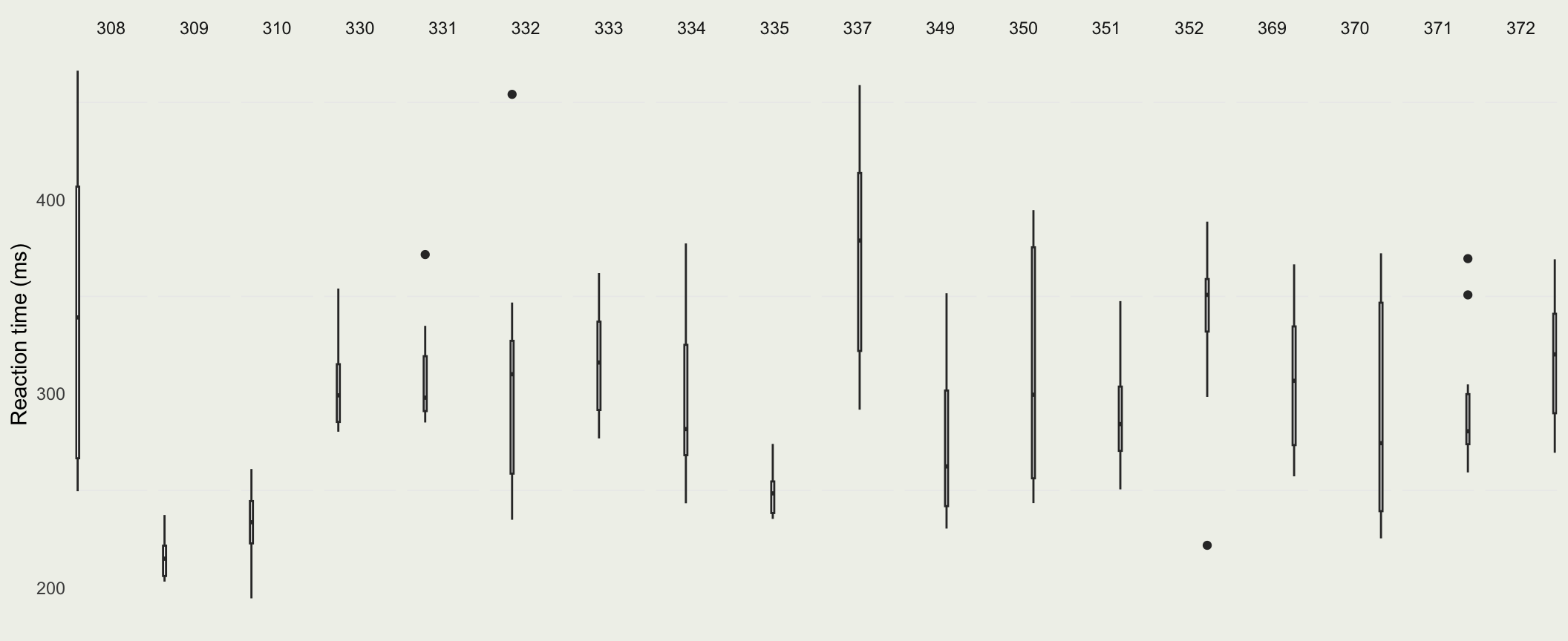
Pooling

• Pooling has to do with how much regularization we induce on parameter estimates in each cluster; sometimes this is called shrinkage
• Complete pooling ignores the clusters and estimates a global parameter
• Even though reaction time \(y_i\), belongs to subject \(j\), we ignore the groups and index all the \(y\)s together

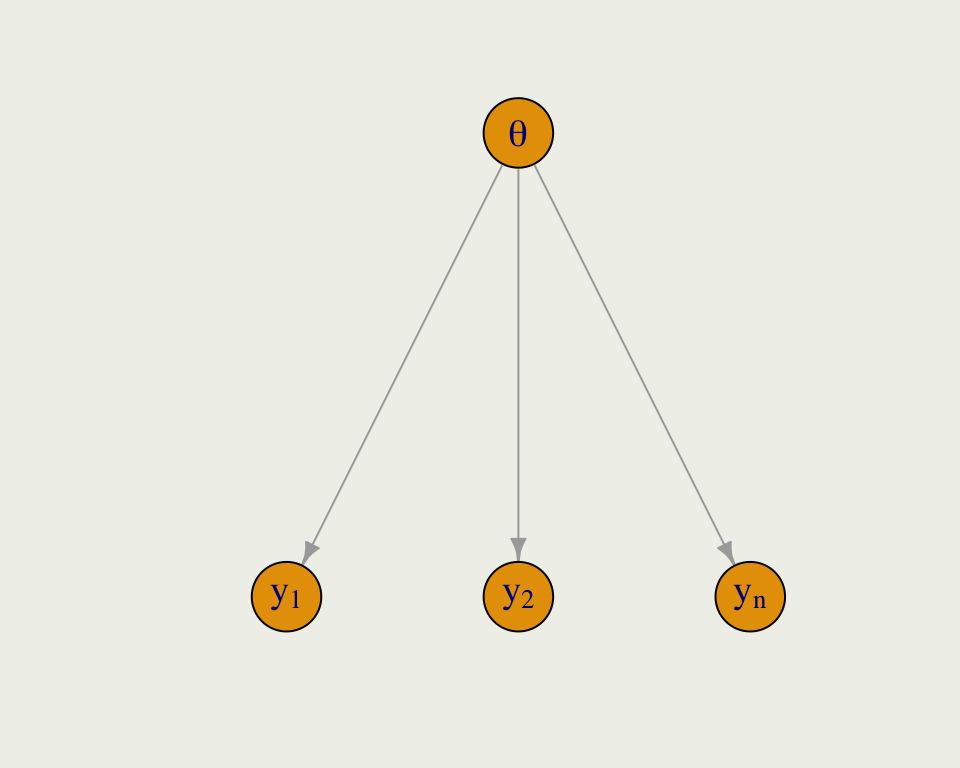
Pooling

• Complete pooling is the opposite of no pooling, where we estimate a separate model for each group
• Here, we have \(n\) subjects, and \(y_{ij}\) refers to the \(i\)th reaction time in subject \(j\)

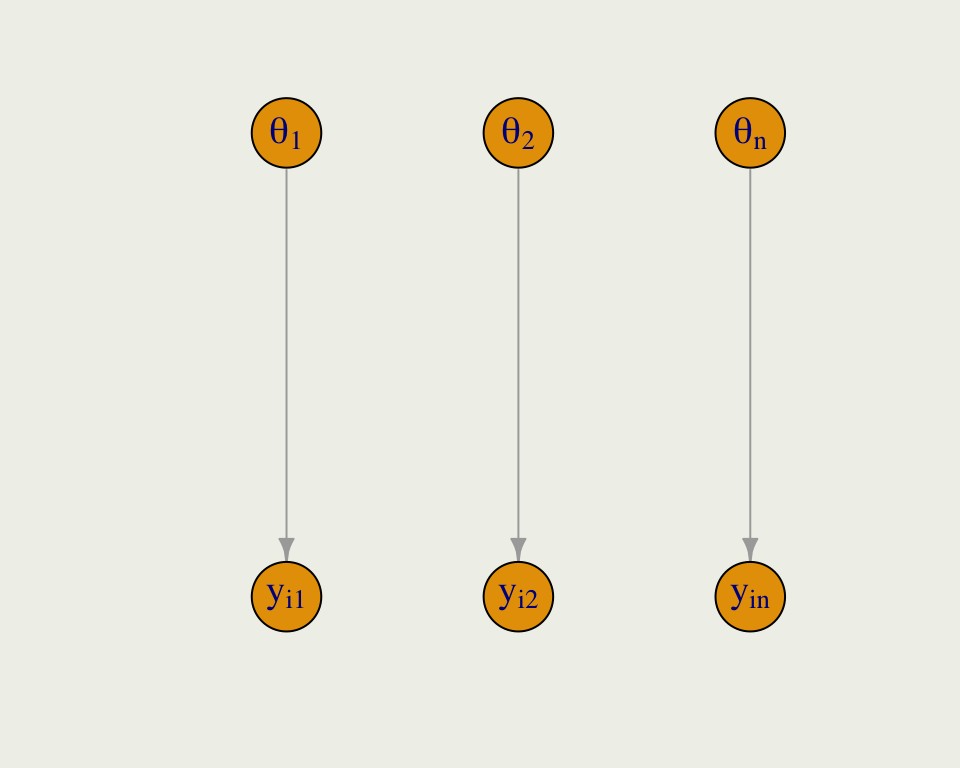
Partial Pooling

• Partial pooling is the compromise between the two extremes
• Like any other parameter in a Bayesian model, the global hyperparameter \(\tau\) is given a prior and is learned from the data
• There could be multiple levels of nesting, say students within schools, within states, etc.

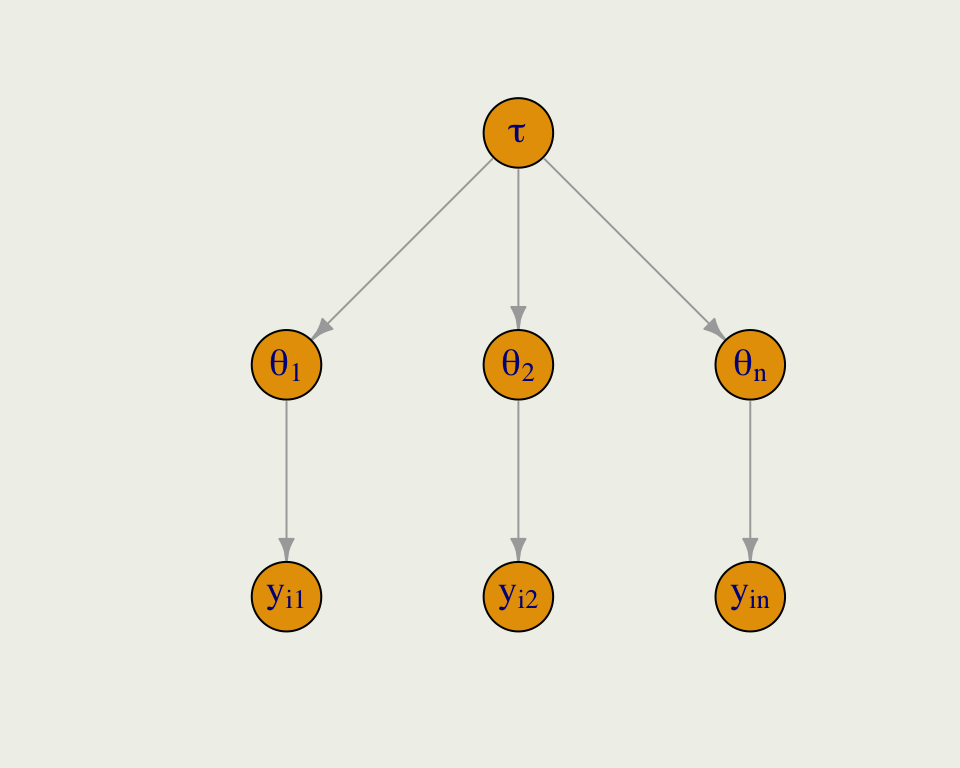
Partial Pooling Compromise

• Posterior \(f(\theta \mid y)\) is is a compromise between prior \(f(\theta)\) and likelihood \(f(y \mid \theta)\)
• In the same spirit, the pooled parameter \(\theta_j\) (say reaction time for subject \(j\)) is a compromise between within-subject parameters, and among-subject parameters

\[ \theta_j \approx \frac{\frac{n_j}{\sigma_{y}^2} \overline y_j + \frac{1}{\sigma_{\tau}^2} \overline y_{\tau}} {\frac{n_j}{\sigma_{y}^2} + \frac{1}{\sigma_{\tau}^2}} \]

• \(\overline y_j\) is no-pool estimate of average reaction time for subject \(j\), and \(\overline y_{\tau}\) is complete-pool estimate
• \(n_j\) is the number of observations for subject \(j\), \(\sigma_{y}^2\) is within subject variance of reaction times, and \(\sigma_{\tau}^2\) is the between-subject variance

Sleep Data

• Let’s build three models for the sleep data, starting with complete pooling, which is what we have been doing all along
• We will start with the intercept-only model
• These data contain the same number of observations per Subject, which is unusual, so we will make it more realistic by removing 30% of the measurements

set.seed(123)
n <- nrow(lme4::sleepstudy)
s <- sample(1:n, n * 0.7)
d <- lme4::sleepstudy[s, ] 
p1 <- ggplot(aes(Days, Reaction), 
            data = d)
p1 <- p1 + geom_jitter(size = 0.3, width = 0.2)
p2 <- ggplot(aes(Reaction), 
            data = d)
p2 <- p2 + geom_histogram(binwidth = 20)
grid.arrange(p1, p2, nrow = 2)

Sleep Data

• This is a simple model of the mean reaction time \(\mu\)

\[ \begin{eqnarray} y_{ij} & \sim & \text{Normal}(\mu, \ \sigma^2) \\ \mu & \sim & \text{Normal}(300, 10^2) \\ \sigma & \sim & \text{Exponential}(0.02) \end{eqnarray} \]

m1 <- stan_glm(Reaction ~ 1,
               prior_intercept = normal(300, 10),
               prior_aux = exponential(0.02),
               family = gaussian,
               data = d, 
               iter = 5000,
               refresh = 0,
               seed = 123)
summary(m1)

Model Info:

 function:     stan_glm
 family:       gaussian [identity]
 formula:      Reaction ~ 1
 algorithm:    sampling
 sample:       10000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 125
 predictors:   1

Estimates:
              mean   sd    10%   50%   90%
(Intercept) 294.5    4.2 289.2 294.5 299.9
sigma        52.9    3.4  48.7  52.7  57.3

Fit Diagnostics:
           mean   sd    10%   50%   90%
mean_PPD 294.4    6.3 286.4 294.4 302.5

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.1  1.0  6347 
sigma         0.0  1.0  6890 
mean_PPD      0.1  1.0  8264 
log-posterior 0.0  1.0  4152 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Sleep Data

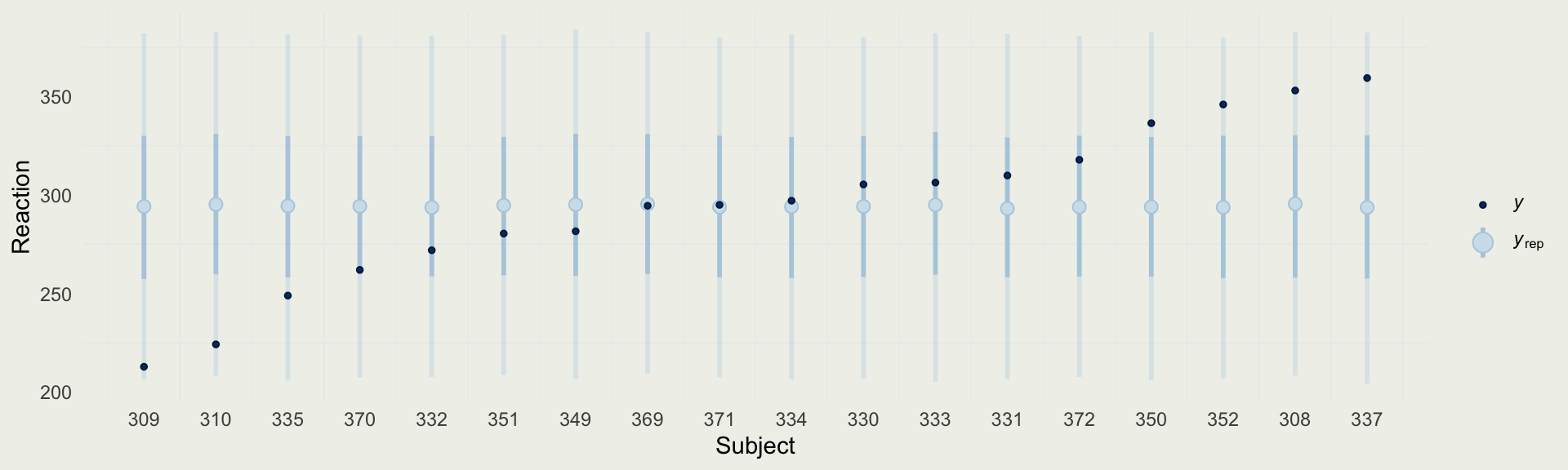
• We can compare the predictions from the complete-pooling model to the reaction times of each subject

new <- d |> group_by(Subject) |> summarise(Reaction = mean(Reaction)) |>
  arrange(Reaction)
new_pred <- posterior_predict(m1, newdata = new)
ppc_intervals(new$Reaction, yrep = new_pred) +
  scale_x_continuous(labels = new$Subject,  breaks = 1:nrow(new)) +
  xlab("Subject") + ylab("Reaction")

Sleep Data

• Next, we will fit a no-pool model, which means we are fitting 18 separate models, one for each subject
• You can fit them separately, by making 18 calls to stan_glm, or you can do in all at once
• Since we will not run 18 separate regressions, it will be simpler to estimate one global variance parameter \(\sigma\), which means there is some variance pooling
• This will not affect the inferences for \(\mu_j\) which is our main focus here

\[ \begin{eqnarray} y_{ij} & \sim & \text{Normal}(\mu_j, \ \sigma^2) \\ \mu_j & \sim & \text{Normal}(300, s_j^2) \\ \sigma & \sim & \text{Exponential}(0.02) \end{eqnarray} \]

Sleep Data

m2 <- stan_glm(Reaction ~ Subject - 1,
               prior = normal(300, 10, autoscale = TRUE),
               prior_aux = exponential(0.02),
               family = gaussian,
               data = d, 
               iter = 1000,
               refresh = 0,
               seed = 123)
summary(m2)

Model Info:

 function:     stan_glm
 family:       gaussian [identity]
 formula:      Reaction ~ Subject - 1
 algorithm:    sampling
 sample:       2000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 125
 predictors:   18

Estimates:
             mean   sd    10%   50%   90%
Subject308 353.4   17.1 331.0 353.8 375.1
Subject309 213.0   14.6 194.4 212.8 231.8
Subject310 223.9   12.9 207.0 224.0 240.2
Subject330 305.2   12.7 288.6 305.1 321.6
Subject331 310.0   15.3 290.1 310.2 329.3
Subject332 272.0   15.2 252.6 271.8 291.7
Subject333 306.1   16.9 284.3 306.0 327.7
Subject334 296.9   12.2 281.1 297.1 312.5
Subject335 248.6   13.2 231.4 248.8 265.1
Subject337 359.4   14.3 341.2 359.4 378.3
Subject349 282.0   15.6 262.2 282.0 301.1
Subject350 336.6   14.5 317.6 336.7 354.8
Subject351 280.5   18.3 256.7 280.8 303.6
Subject352 346.1   16.5 325.2 345.9 367.1
Subject369 294.7   14.3 276.4 294.6 313.6
Subject370 262.1   14.9 243.7 262.2 281.4
Subject371 295.4   11.7 280.3 295.2 309.9
Subject372 317.6   11.9 302.7 317.6 333.0
sigma       37.4    2.6  34.4  37.2  40.7

Fit Diagnostics:
           mean   sd    10%   50%   90%
mean_PPD 293.2    4.8 287.1 293.2 299.2

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
              mcse Rhat n_eff
Subject308    0.3  1.0  2742 
Subject309    0.3  1.0  3019 
Subject310    0.3  1.0  2411 
Subject330    0.3  1.0  2263 
Subject331    0.3  1.0  2563 
Subject332    0.3  1.0  2924 
Subject333    0.3  1.0  2560 
Subject334    0.2  1.0  2928 
Subject335    0.2  1.0  3386 
Subject337    0.3  1.0  2424 
Subject349    0.3  1.0  2629 
Subject350    0.3  1.0  2490 
Subject351    0.4  1.0  2272 
Subject352    0.3  1.0  2909 
Subject369    0.3  1.0  2915 
Subject370    0.3  1.0  2594 
Subject371    0.2  1.0  2399 
Subject372    0.2  1.0  2760 
sigma         0.1  1.0  1113 
mean_PPD      0.1  1.0  2215 
log-posterior 0.1  1.0   719 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Sleep Data

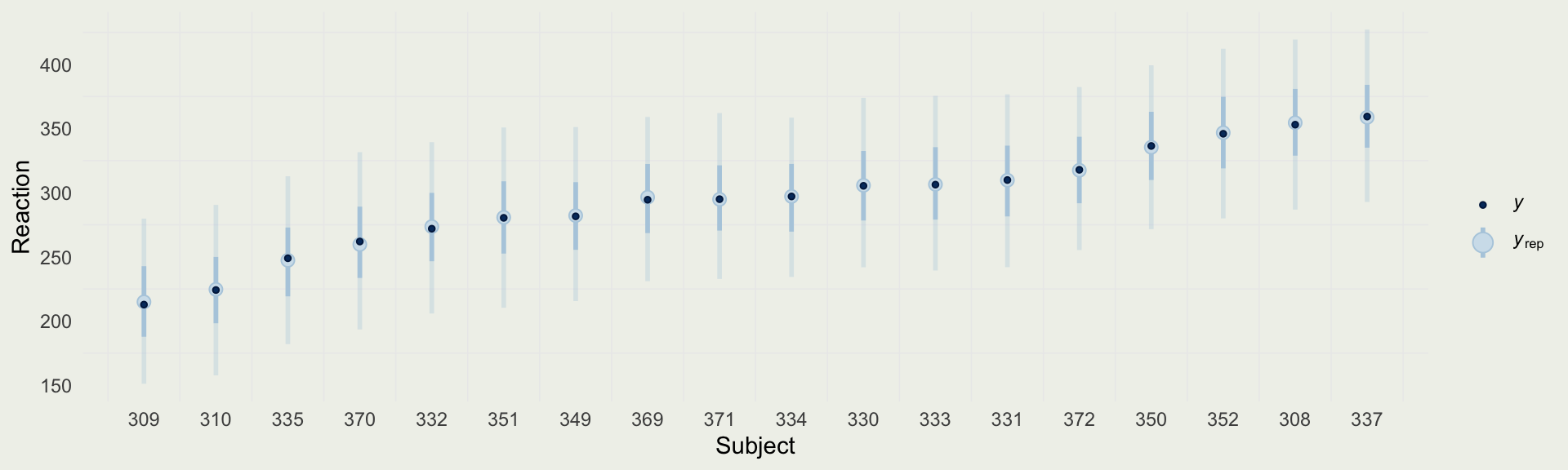
• We can compare the predictions from the no-pooling model to the reaction times of each subject

new_pred <- posterior_predict(m2, newdata = new)
ppc_intervals(new$Reaction, yrep = new_pred) +
  scale_x_continuous(labels = new$Subject,  breaks = 1:nrow(new)) +
  xlab("Subject") + ylab("Reaction")

• What are some of the limitations of this approach?

Building a Hierarchical Model

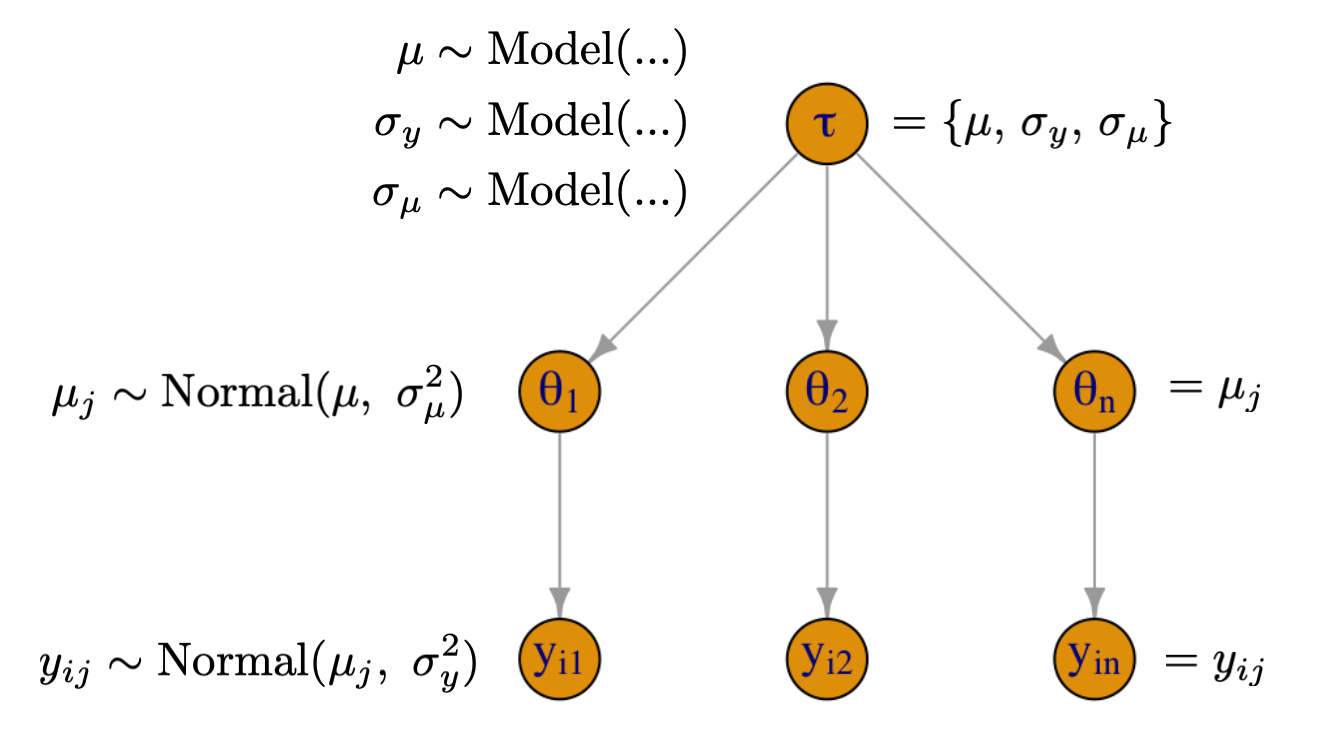
• \(\mu_j\) is an average reaction time for subject \(j\)
• \(\sigma_y\) is the within-subject variability of reaction times
• \(\mu\) is the global average of reaction times across all subject
• \(\sigma_{\mu}\) is subject to subject variability of reaction times
• Top-level parameters get fixed priors and induce the degree of pooling

Sleep Data

• We can now write out the full model giving priors to all global parameters
• Notice, how the model could be extended if instead of \(\mu_j\) we had our typical linear predictor

\[ \begin{eqnarray} y_{ij} &\sim& \text{Normal}(\mu_j, \ \sigma_y^2) \\ \mu_{j} &\sim& \text{Normal}(\mu, \ \sigma_{\mu}^2) \\ \mu &\sim& \text{Normal}(300, 50^2) \\ \sigma_y &\sim& \text{Exponential}(0.02) \\ \sigma_{\mu} &\sim& \text{Exponential}(1) \end{eqnarray} \]

• This model can also be written such that \(\mu_j = \mu + b_j\), where each \(b_j \sim \text{Normal}(0, \sigma_{\mu}^2)\)

Sleep Data

m3 <- stan_glmer(Reaction ~ (1 | Subject),
                 prior_intercept = normal(300, 50),
                 prior_aux = exponential(0.02),
                 prior_covariance = decov(reg = 1, 
                   conc = 1, shape = 1, scale = 1),
                 family = gaussian, data = d, iter = 1500,
                 refresh = 0,
                 seed = 123)

• (Intercept) = \(\mu\)
• sigma = \(\sigma_y\)
• Sigma[Subject:(Intercept),(Intercept)] = \(\sigma^2_{\mu}\)
• b[(Intercept) Subject:XYZ] = \(b_j\), and so \(\mu_j = \mu + \beta_j\)

summary(m3)

Model Info:

 function:     stan_glmer
 family:       gaussian [identity]
 formula:      Reaction ~ (1 | Subject)
 algorithm:    sampling
 sample:       3000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 125
 groups:       Subject (18)

Estimates:
                                         mean   sd     10%    50%    90% 
(Intercept)                             294.2    9.8  281.8  294.5  306.5
b[(Intercept) Subject:308]               49.3   17.5   27.3   49.0   71.5
b[(Intercept) Subject:309]              -71.7   16.5  -92.5  -71.5  -50.8
b[(Intercept) Subject:310]              -62.7   15.1  -82.3  -62.5  -43.9
b[(Intercept) Subject:330]               10.0   15.0   -8.8    9.8   29.0
b[(Intercept) Subject:331]               13.3   16.4   -7.2   13.4   33.9
b[(Intercept) Subject:332]              -19.2   16.4  -39.7  -19.1    2.1
b[(Intercept) Subject:333]                9.8   18.0  -13.0    9.8   32.4
b[(Intercept) Subject:334]                2.7   14.8  -16.2    2.6   21.6
b[(Intercept) Subject:335]              -40.4   15.4  -60.1  -40.2  -21.1
b[(Intercept) Subject:337]               57.4   16.1   37.2   57.2   77.4
b[(Intercept) Subject:349]              -10.8   16.3  -31.4  -10.8    9.9
b[(Intercept) Subject:350]               37.1   15.5   17.3   37.1   56.8
b[(Intercept) Subject:351]              -10.9   18.2  -34.6  -11.0   12.7
b[(Intercept) Subject:352]               43.1   17.3   21.1   42.8   65.0
b[(Intercept) Subject:369]                0.5   16.3  -20.3    0.3   21.2
b[(Intercept) Subject:370]              -28.2   16.3  -48.9  -28.3   -6.9
b[(Intercept) Subject:371]                0.7   14.3  -17.1    0.6   19.3
b[(Intercept) Subject:372]               21.3   14.1    3.8   21.3   39.0
sigma                                    37.5    2.5   34.3   37.4   40.8
Sigma[Subject:(Intercept),(Intercept)] 1685.8  706.9  968.5 1538.3 2541.1

Fit Diagnostics:
           mean   sd    10%   50%   90%
mean_PPD 293.0    4.9 286.8 292.9 299.4

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
                                       mcse Rhat n_eff
(Intercept)                             0.5  1.0  383 
b[(Intercept) Subject:308]              0.5  1.0 1285 
b[(Intercept) Subject:309]              0.5  1.0 1171 
b[(Intercept) Subject:310]              0.5  1.0  987 
b[(Intercept) Subject:330]              0.5  1.0  821 
b[(Intercept) Subject:331]              0.6  1.0  889 
b[(Intercept) Subject:332]              0.5  1.0 1103 
b[(Intercept) Subject:333]              0.5  1.0 1267 
b[(Intercept) Subject:334]              0.5  1.0  797 
b[(Intercept) Subject:335]              0.5  1.0 1092 
b[(Intercept) Subject:337]              0.5  1.0  965 
b[(Intercept) Subject:349]              0.5  1.0 1196 
b[(Intercept) Subject:350]              0.5  1.0  885 
b[(Intercept) Subject:351]              0.4  1.0 1648 
b[(Intercept) Subject:352]              0.5  1.0 1246 
b[(Intercept) Subject:369]              0.5  1.0  928 
b[(Intercept) Subject:370]              0.5  1.0 1020 
b[(Intercept) Subject:371]              0.5  1.0  819 
b[(Intercept) Subject:372]              0.5  1.0  754 
sigma                                   0.0  1.0 2630 
Sigma[Subject:(Intercept),(Intercept)] 23.6  1.0  895 
mean_PPD                                0.1  1.0 3211 
log-posterior                           0.2  1.0  617 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Computing \(\mu_j\)

muj <- m3 |>
  spread_draws(`(Intercept)`, b[ ,Subject]) |>
  mutate(mu_j = `(Intercept)` + b) |>
  select(Subject, mu_j) |>
  mean_qi(.width = 0.90)

head(muj)

# A tibble: 6 × 7
  Subject      mu_j .lower .upper .width .point .interval
  <chr>       <dbl>  <dbl>  <dbl>  <dbl> <chr>  <chr>    
1 Subject:308  344.   318.   369.    0.9 mean   qi       
2 Subject:309  223.   200.   245.    0.9 mean   qi       
3 Subject:310  231.   211.   252.    0.9 mean   qi       
4 Subject:330  304.   285.   324.    0.9 mean   qi       
5 Subject:331  308.   284.   330.    0.9 mean   qi       
6 Subject:332  275.   252.   298.    0.9 mean   qi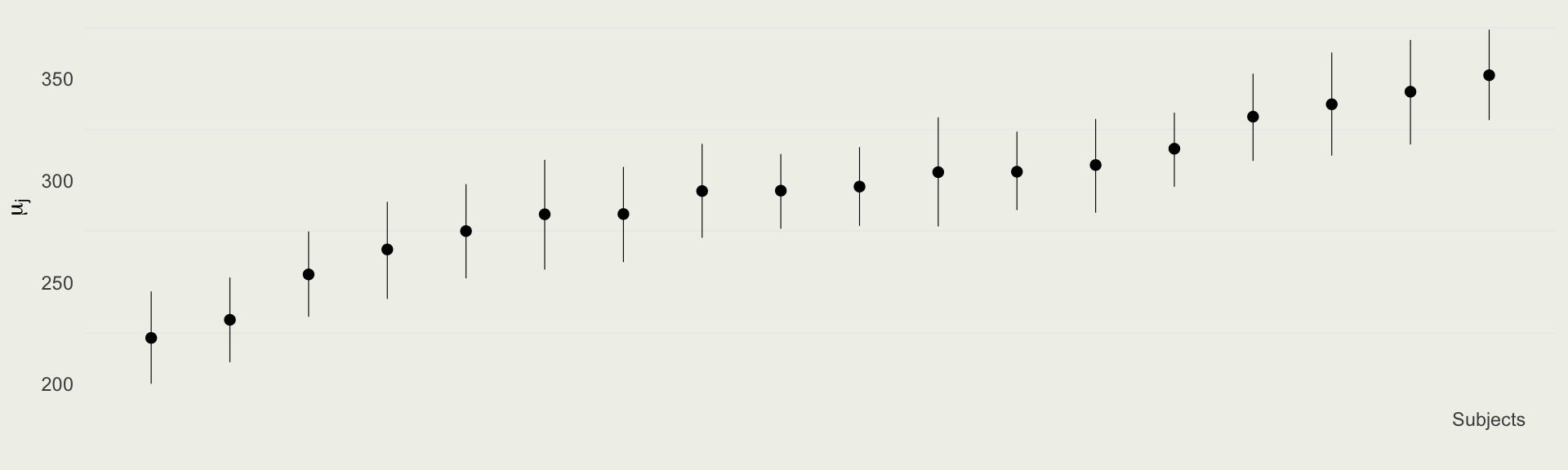       

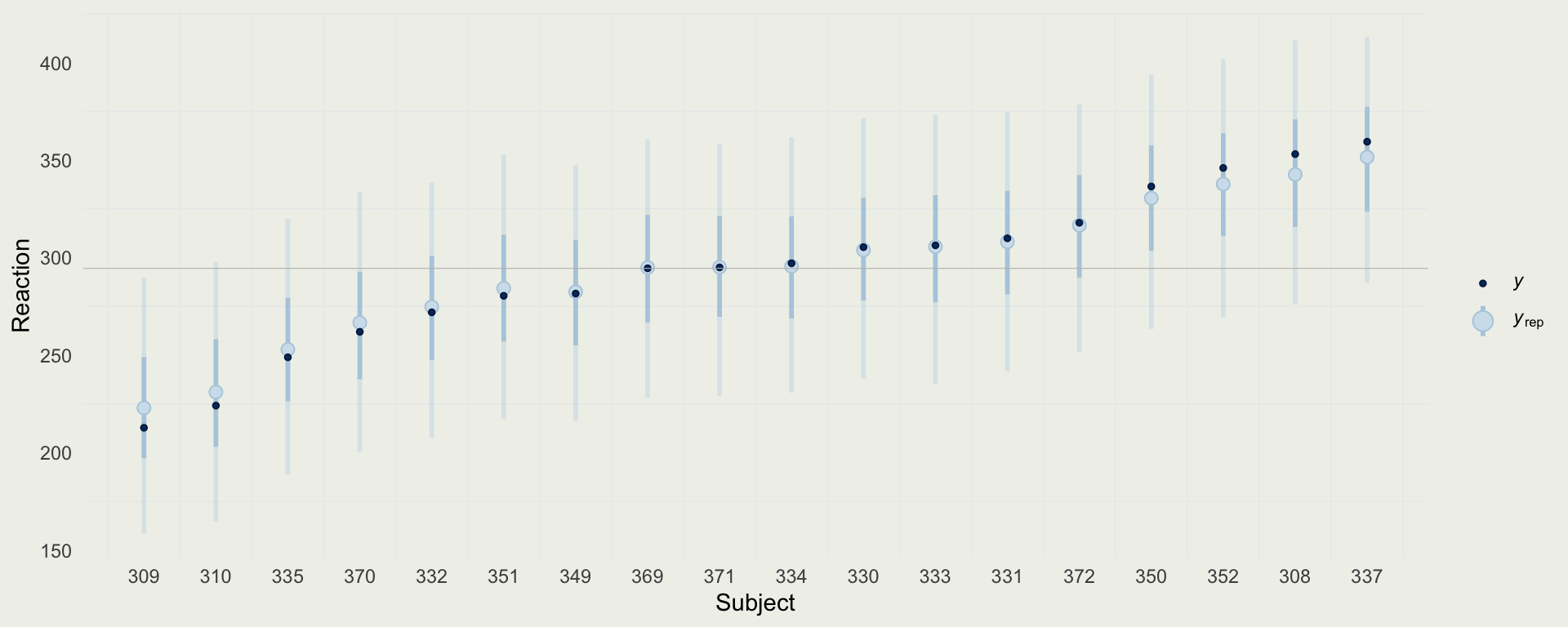
Sleep Data

• We can see the effects of hierarchical pooling below
• Subjects that are farther away from \(\E(\mu) = 294\)(ms) and the ones that have fewer observations are pooled more towards the global mean

Building a Full Hierarchical Model

• The model we have built so far is for average reaction time only
• What we would like to do, is to build a pooled regression model for the reaction time of each subject
• The mechanics are similar but now we need a model for the slopes and intercepts for each subject, their covariance, and priors

m4 <- stan_glmer(Reaction ~ Days + (Days | Subject),
                 prior_intercept = normal(300, 50),
                 prior = normal(0, 2, autoscale = TRUE),
                 prior_aux = exponential(0.02),
                 prior_covariance = decov(reg = 1, 
                   conc = 1, shape = 1, scale = 1),
                 family = gaussian, data = d, iter = 1500,
                 cores = 4, seed = 123, refresh = 0)
summary(m4)

Model Info:

 function:     stan_glmer
 family:       gaussian [identity]
 formula:      Reaction ~ Days + (Days | Subject)
 algorithm:    sampling
 sample:       3000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 125
 groups:       Subject (18)

Estimates:
                                         mean   sd     10%    50%    90% 
(Intercept)                             256.3    7.7  246.6  256.2  265.9
Days                                      8.9    1.7    6.7    8.9   11.1
b[(Intercept) Subject:308]               42.1   22.7   15.0   39.7   72.8
b[Days Subject:308]                       0.9    4.4   -4.9    1.2    6.2
b[(Intercept) Subject:309]              -43.1   14.0  -61.2  -43.0  -25.6
b[Days Subject:309]                      -7.9    3.1  -11.8   -7.9   -3.8
b[(Intercept) Subject:310]              -42.8   13.5  -60.4  -42.3  -26.0
b[Days Subject:310]                      -5.0    2.9   -8.7   -5.0   -1.3
b[(Intercept) Subject:330]               23.8   14.4    5.7   23.3   42.0
b[Days Subject:330]                      -4.1    2.8   -7.8   -4.0   -0.6
b[(Intercept) Subject:331]               19.2   12.9    3.0   19.0   35.8
b[Days Subject:331]                       0.7    2.9   -3.1    0.7    4.4
b[(Intercept) Subject:332]                2.8   12.6  -12.8    2.3   19.2
b[Days Subject:332]                      -5.1    2.9   -8.9   -5.0   -1.4
b[(Intercept) Subject:333]               11.7   14.9   -7.0   11.2   31.0
b[Days Subject:333]                       0.3    3.1   -3.7    0.4    4.2
b[(Intercept) Subject:334]               -9.7   13.2  -26.9   -9.3    7.0
b[Days Subject:334]                       2.4    2.7   -1.0    2.4    5.8
b[(Intercept) Subject:335]               -7.2   14.4  -25.5   -7.5   11.5
b[Days Subject:335]                      -8.9    2.8  -12.5   -8.9   -5.2
b[(Intercept) Subject:337]               32.9   13.6   15.6   32.9   50.4
b[Days Subject:337]                       9.9    3.0    6.0    9.9   13.7
b[(Intercept) Subject:349]              -25.4   18.1  -49.2  -24.0   -3.1
b[Days Subject:349]                       1.5    3.4   -2.9    1.4    6.0
b[(Intercept) Subject:350]              -10.7   16.7  -32.6  -10.1   10.6
b[Days Subject:350]                       8.1    3.1    4.3    8.0   12.3
b[(Intercept) Subject:351]                3.2   16.9  -17.9    2.7   24.5
b[Days Subject:351]                      -4.1    3.7   -8.8   -4.0    0.5
b[(Intercept) Subject:352]               26.9   16.4    6.8   26.4   47.7
b[Days Subject:352]                       3.4    3.2   -0.7    3.5    7.4
b[(Intercept) Subject:369]               -0.4   13.1  -17.0   -0.4   15.6
b[Days Subject:369]                       1.1    2.8   -2.4    1.1    4.7
b[(Intercept) Subject:370]              -31.5   14.5  -50.2  -31.0  -13.4
b[Days Subject:370]                       5.0    3.5    0.4    5.0    9.5
b[(Intercept) Subject:371]               -1.9   12.8  -18.0   -1.8   14.3
b[Days Subject:371]                       0.1    2.6   -3.1    0.1    3.4
b[(Intercept) Subject:372]               10.2   12.6   -5.7   10.3   26.5
b[Days Subject:372]                       2.4    2.6   -0.9    2.4    5.7
sigma                                    22.1    1.8   20.0   22.0   24.4
Sigma[Subject:(Intercept),(Intercept)]  845.2  460.0  381.3  751.0 1416.9
Sigma[Subject:Days,(Intercept)]           9.2   64.9  -68.9   14.1   77.8
Sigma[Subject:Days,Days]                 44.8   22.7   22.0   39.6   73.6

Fit Diagnostics:
           mean   sd    10%   50%   90%
mean_PPD 293.3    2.8 289.8 293.2 296.9

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
                                       mcse Rhat n_eff
(Intercept)                             0.2  1.0 1300 
Days                                    0.0  1.0 1246 
b[(Intercept) Subject:308]              0.6  1.0 1616 
b[Days Subject:308]                     0.1  1.0 1862 
b[(Intercept) Subject:309]              0.3  1.0 2340 
b[Days Subject:309]                     0.1  1.0 2460 
b[(Intercept) Subject:310]              0.3  1.0 1957 
b[Days Subject:310]                     0.1  1.0 2338 
b[(Intercept) Subject:330]              0.4  1.0 1533 
b[Days Subject:330]                     0.1  1.0 1666 
b[(Intercept) Subject:331]              0.3  1.0 2157 
b[Days Subject:331]                     0.1  1.0 2760 
b[(Intercept) Subject:332]              0.3  1.0 1876 
b[Days Subject:332]                     0.1  1.0 2272 
b[(Intercept) Subject:333]              0.3  1.0 2132 
b[Days Subject:333]                     0.1  1.0 2255 
b[(Intercept) Subject:334]              0.3  1.0 1935 
b[Days Subject:334]                     0.1  1.0 1922 
b[(Intercept) Subject:335]              0.3  1.0 1693 
b[Days Subject:335]                     0.1  1.0 1648 
b[(Intercept) Subject:337]              0.3  1.0 2140 
b[Days Subject:337]                     0.1  1.0 2307 
b[(Intercept) Subject:349]              0.4  1.0 1636 
b[Days Subject:349]                     0.1  1.0 1769 
b[(Intercept) Subject:350]              0.4  1.0 1649 
b[Days Subject:350]                     0.1  1.0 1450 
b[(Intercept) Subject:351]              0.4  1.0 2235 
b[Days Subject:351]                     0.1  1.0 2194 
b[(Intercept) Subject:352]              0.3  1.0 2721 
b[Days Subject:352]                     0.1  1.0 2473 
b[(Intercept) Subject:369]              0.3  1.0 2130 
b[Days Subject:369]                     0.1  1.0 2044 
b[(Intercept) Subject:370]              0.4  1.0 1427 
b[Days Subject:370]                     0.1  1.0 1486 
b[(Intercept) Subject:371]              0.3  1.0 1885 
b[Days Subject:371]                     0.1  1.0 2096 
b[(Intercept) Subject:372]              0.3  1.0 2141 
b[Days Subject:372]                     0.1  1.0 1802 
sigma                                   0.0  1.0 1532 
Sigma[Subject:(Intercept),(Intercept)] 13.9  1.0 1099 
Sigma[Subject:Days,(Intercept)]         2.1  1.0  931 
Sigma[Subject:Days,Days]                0.6  1.0 1364 
mean_PPD                                0.1  1.0 2854 
log-posterior                           0.3  1.0  518 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Building a Full Hierarchical Model

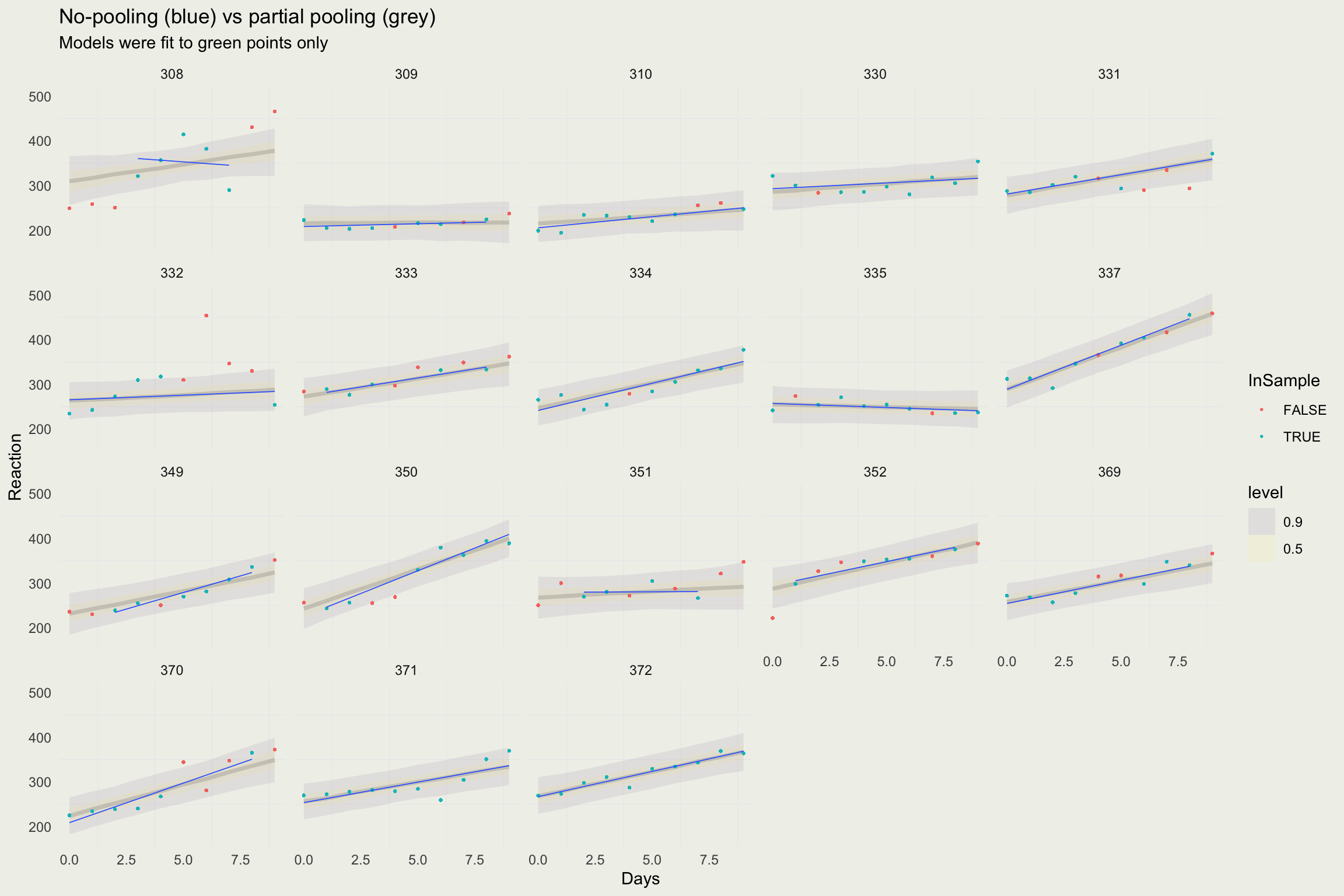
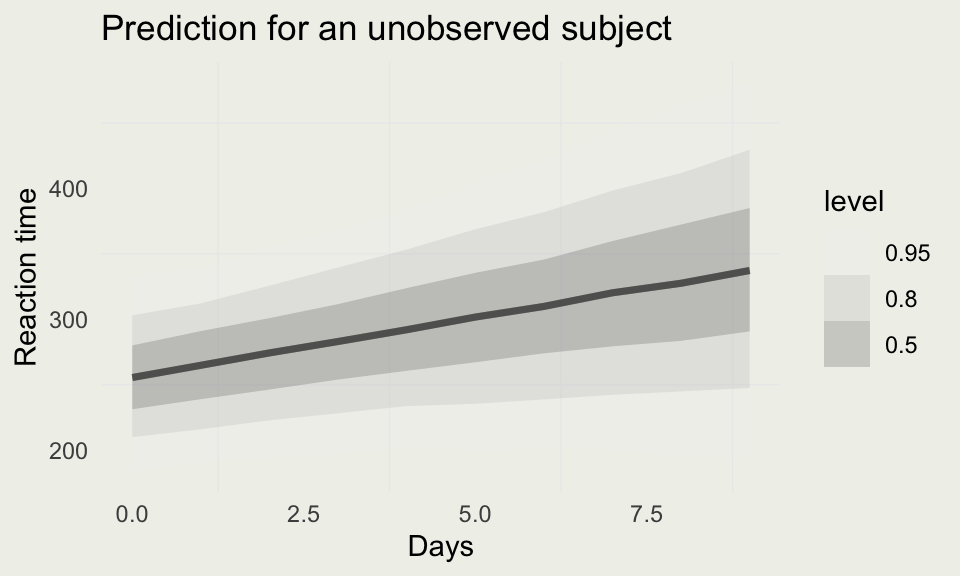
Predicting for a New Subject

• We saw that we can make predictions for reaction times of subjects that were part of the model
• But we can also make predictions for unobserved subjects by drawing from the “population” distribution, as opposed to subject-specific parameters

new_subj <- data.frame(Days = 0:9, 
              Subject = as.factor(rep(400, 10)))
ypred_subj <- posterior_predict(m4, 
                        newdata = new_subj)
new_subj |>
  add_predicted_draws(m4) |>
  ggplot(aes(x = Days)) +
  stat_lineribbon(aes(y = .prediction), 
                  width = c(.9, .8, .5), 
                  alpha = 0.25) +
  ylab("Reaction time") + 
  ggtitle("Prediction for an unobserved subject") +
  scale_fill_brewer(palette = "Greys")

Course Evaluations