SMaC: Statistics, Math, and Computing
APSTA-GE 2006: Applied Statistics for Social Science Research
Session 2 Outline
Linear, exponential, and logarithmic functions
Limits
Definition of the derivative
Rules of differentiation
The chain rule and product rules
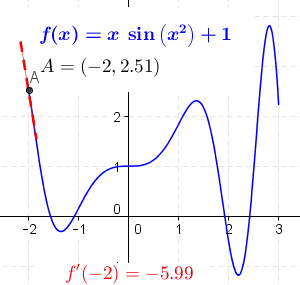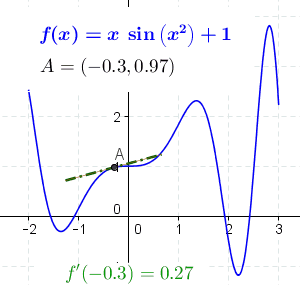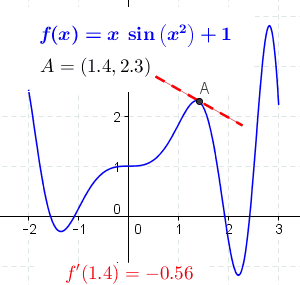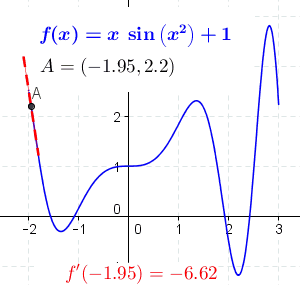
Image source: Wikipedia
Lines
- We typically use the slope-intercept form of the line: \(y = a + bx\), where \(a\) is the intercept, and \(b\) is the slope (rise over run).
- For example: \(y = 1.5 + 0.5x\)
- \(1.5\) is the value of the function when either \(x = 0\) or \(b = 0\).
- In practice, \(b\) is almost never zero.
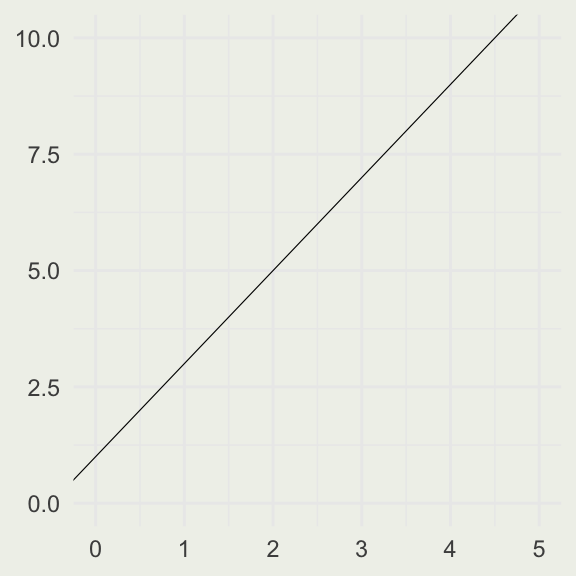
A graph of a line with the equation \(y = 1 + 2x\).
A graph of a line with the equation \(y = 7.5 - 2x\).
Your Turn
- Turn the following code into a function called
plot_line(slope, intercept) - Test it for different values of
slopeandintercept
Exponential Functions
- The idea of an exponential function is that the rate of change of the function at time \(t\) is proportional to the value of the function at time \(t\). In other words:
\[ \frac{\text{d}[y(t)]}{\text{d}t} = k \cdot y(t) \]
The solution to this differential equation is the exponential function.
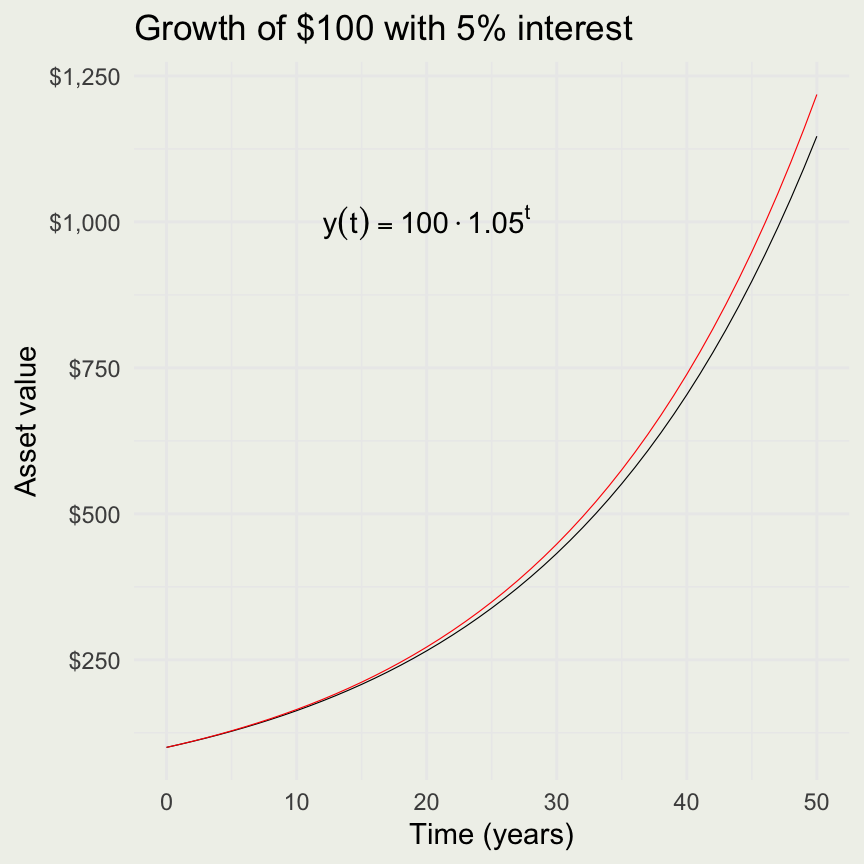
Think of population growth or growth of an interest-bearing asset.
Example: Compound Interest
An asset that has a value \(A\) is invested with an annual interest rate \(r\). What is the balance in the account, \(P_1\), at the end of the first year?
\[ P_1 = A + rA = A(1 + r) \]
After year two, the value is:
\[ P_2 = P_1 + rP_1 = P_1(1 + r) = \\ A(1 + r)(1 + r) = A(1 + r)^2 \]
And after year \(t\), the value is:
\[ P_n = A(1 + r)^t \]
What if we compound the interest twice per year? In that case:
\[ P_1 = A \left (1 + \frac{r}{2} \right)^2 \]
If we compound \(n\) times per year, the principal would be:
\[ P_1 = A \left (1 + \frac{r}{n} \right)^n \]
Combining these ideas, if we compound \(n\) times per year, for \(t\) years, we get:
\[ P = A \left (1 + \frac{r}{n} \right)^{nt} \]
If we let \(n \to \infty\), we call this process exponential growth.
Example: Compound Interest
rate <- 0.05 # interest rate r
P <- 100 # pricical P
n_comp <- 1:100 # number of compoundings n
Pn <- function(n, A, r, t) A * (1 + r/n)^(t*n)
Pe <- function(A, r, t) A * exp(r * t)
pn <- Pn(n = n_comp, A = P, r = rate, t = 50)
pe <- Pe(A = P, r = rate, t = 50)
d <- data.frame(n_comp, pn)
p <- ggplot(d, aes(n_comp, pn))
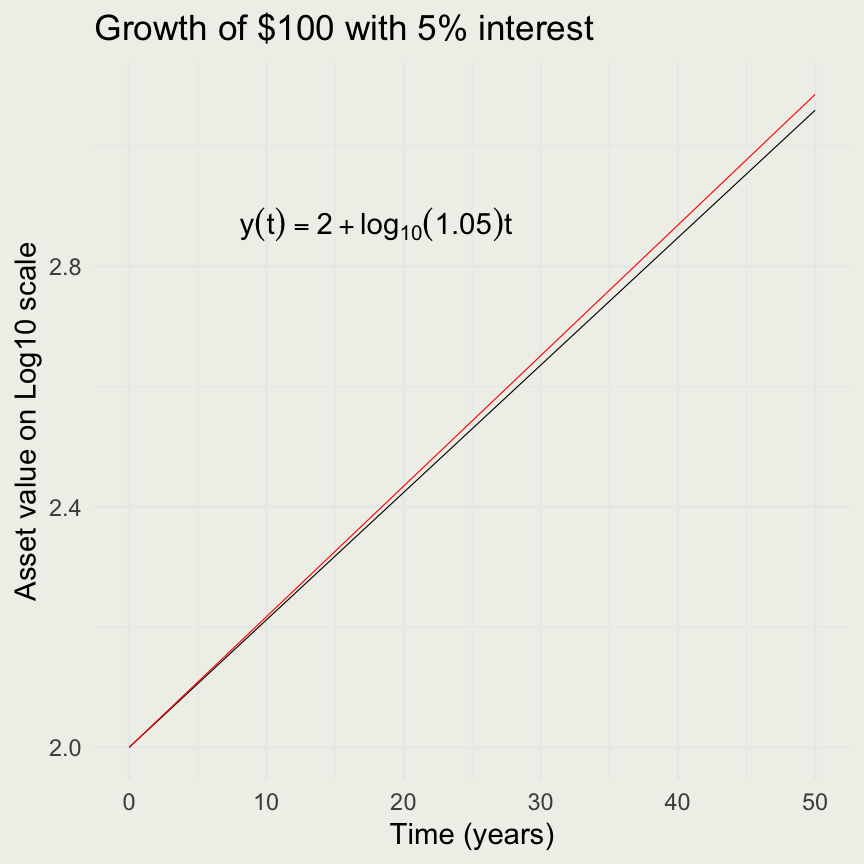
p + geom_line(size = 0.2) +
geom_hline(yintercept = pe, color = 'red', size = 0.2) +
xlab("Number of times the interest is compounded") +
ylab("Value of an asset") +
ggtitle("Value of $100 at r = 0.05 after 50 years") 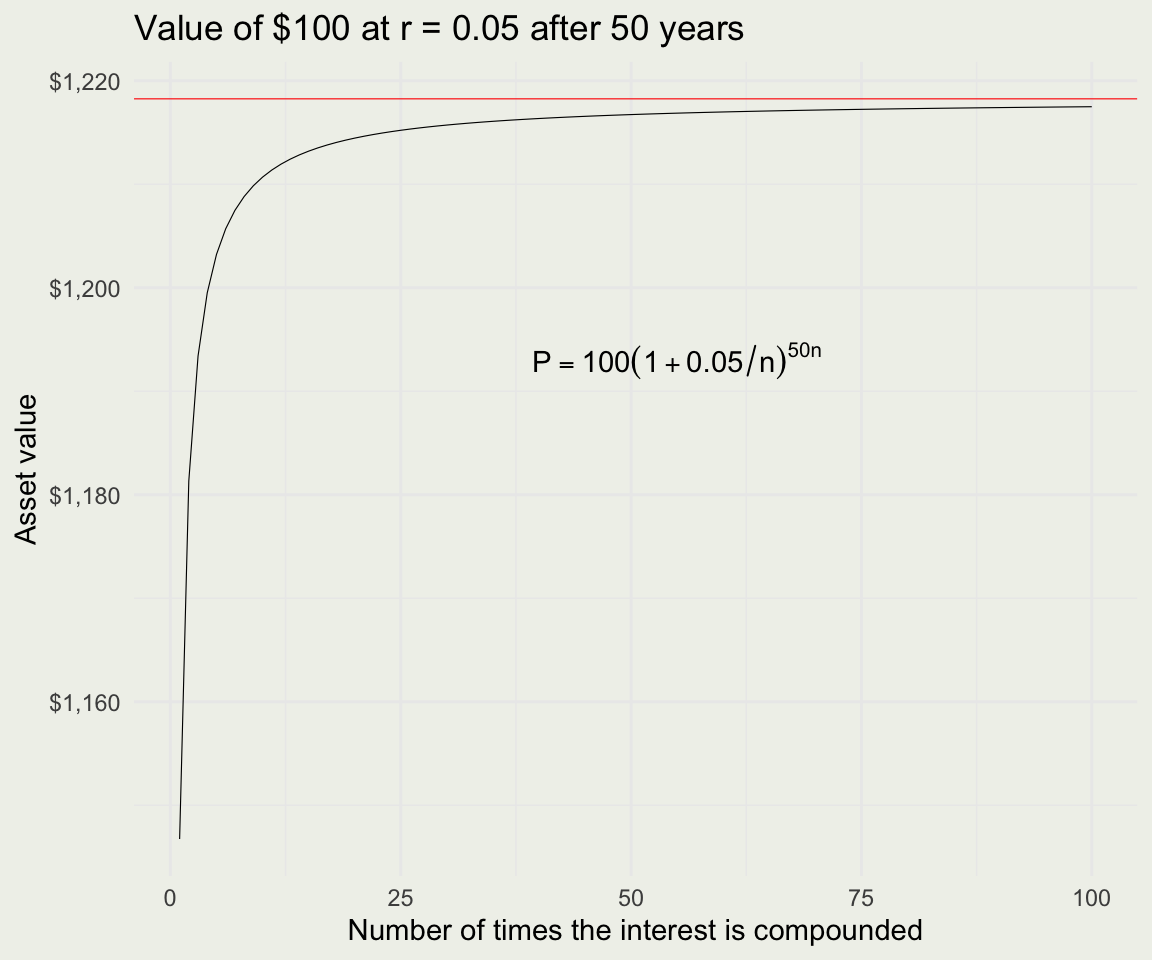
Your Turn
Suppose a particular population of bacteria is known to double in size every 4 hours. If a culture starts with 1000 bacteria, what is the population after 10 hours and 24 hours?
The Number \(e\)
- Recall the equation for asset value after \(t\) years compounded \(n\) times:
\[ P = A \left (1 + \frac{r}{n} \right)^n = A \left (1 + \frac{r}{n} \right)^{nt} \]
- Let’s make a substituion \(m = n/r\) and take limit and \(m \to \infty\).
\[ P = \lim_{m \to \infty}A \left ( 1 + \frac{1}{m} \right)^{m(rt)} \]
The Number \(e\)
- We can compute the value of \(\left ( 1 + \frac{1}{m} \right)^m\) as m increases.
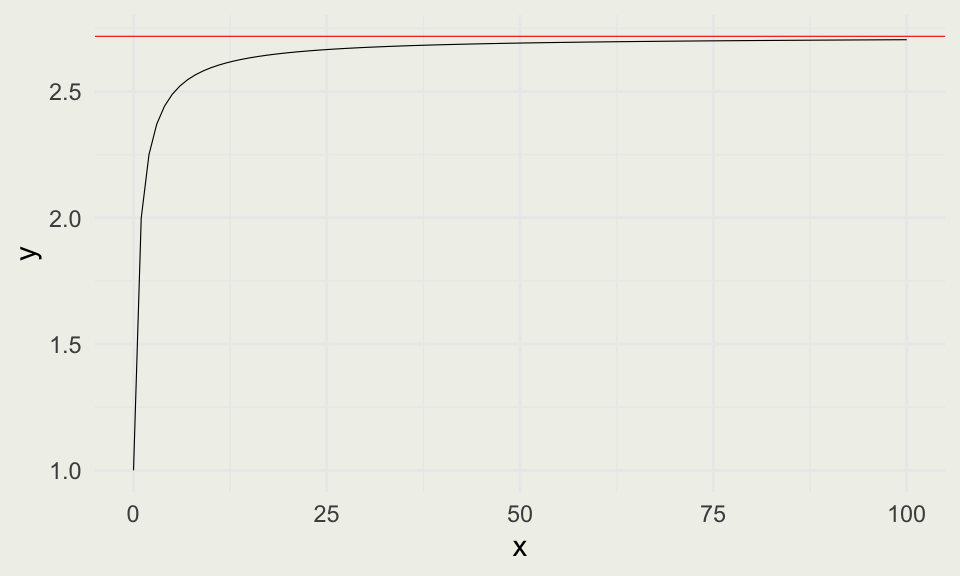
- The number that this limit approaches is called \(e\).
\[ P = \lim_{ m \to \infty}A \left ( 1 + \frac{1}{m} \right)^{m(rt)} = A e^{rt} \]
Properties of Exponents
Your Turn
Suppose $750 is invested in an account at an annual interest rate of 5.5%, compounded continuously. Let \(t\) denote the number of years after the initial investment and \(A(t)\) denote the amount of money in the account at time \(t\). Find a formula for \(A(t)\). Find the amount of money in the account after 5 years, 10 years, and 50 years.
Logarithmic functions
Exponential function of the form \(f(x) = a^x\) is one-to-one, so it has an inverse called a logarithmic function.
In Statistics, when we write \(\log\) we mean natural log, base \(e\). This makes it easier to interpret the log regression coefficients as percentage changes. For example, \(\log(1.04) \approx 4\%\).
The following relationship always holds: \(a^t = e^{\log(a)t}\) since \(e^{\log(a)} = a\)
\(\log_a(uv) = \log_a(u) + \log_a(v)\)
\(\log_a(u/v) = \log_a(u) - \log_a(v)\)
\(\log_a u^n = n \log_a u\)
In statistics and Machine Learning, we often want to normalize a vector so that it adds to one. One such function is called a softmax:
\[ \text{softmax}(x) = \frac{\exp(x)} {\sum_{n=1}^N \exp(x_n)} \]
- If \(x\) is a vector of size 3, the numerator is component-wise \(\exp\) of size 3, the denominator is a scalar, and the function value is a vector of size 3 that adds to 1
[1] 2.718282 7.389056 20.085537[1] 30.19287[1] 0.09003057 0.24472847 0.66524096[1] Inf Inf Inf- This produces overflow – the numbers are too big for the computer. Let’s compute the \(\log \text{softmax}(x)\).
\[ \log\text{softmax}(x) = x - \log \sum_{n=1}^N \exp(x_n) \]
The second term is the log-sum-exp or LSE for short. It has the same problem, as it will overflow or underflow.
The idea is that we need to reduce the magnitude of \(x_n\) while preserving the integrity of the LSE function.
\[ \begin{eqnarray} \text{Let } c & = & \max(x_1, x_2, x_3, ..., x_N) \\ y & = & \log \sum_{n=1}^N \exp(x_n) \\ \exp(y) & = & \sum_{n=1}^N \exp(x_n) \\ \exp(y) & = & \exp(c) \sum_{n=1}^N \exp(x_n - c) \\ y & = & c + \log \sum_{n=1}^N \exp(x_n - c) \end{eqnarray} \]
- Because \(c = \max(x)\), the largest exponent is zero.
- Your Turn: write a function called
LSEthat takes in vector \(x\) and implements the last equation and tests it on small and large values of \(x\). Now implement thesoftmax_logfunction using theLSEfunction. Now compute the same version of the softmax function and check that it sums to 1.
LSE <- function(x) {
c <- max(x)
y <- c + log(sum(exp(x - c)))
return(y)
}
softmax_log <- function(x) {
x - LSE(x)
}
softmax_unsafe <- function(x) exp(x) / sum(exp(x))
softmax_unsafe(1:3)[1] 0.09003057 0.24472847 0.66524096[1] -2.407606 -1.407606 -0.407606[1] 0.09003057 0.24472847 0.66524096[1] 1000 1001 1002[1] NaN NaN NaN[1] 0.09003057 0.24472847 0.66524096[1] 1Limits
The idea of the limit is to evaluate what the function approaches as we increase or decrease the inputs.
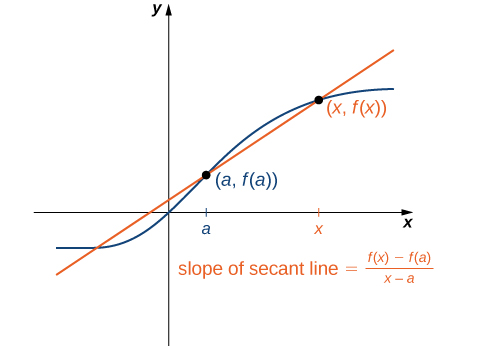
This demo shows what happens to the secant line as it approaches the tangent.
Source: Calculus Volume 1
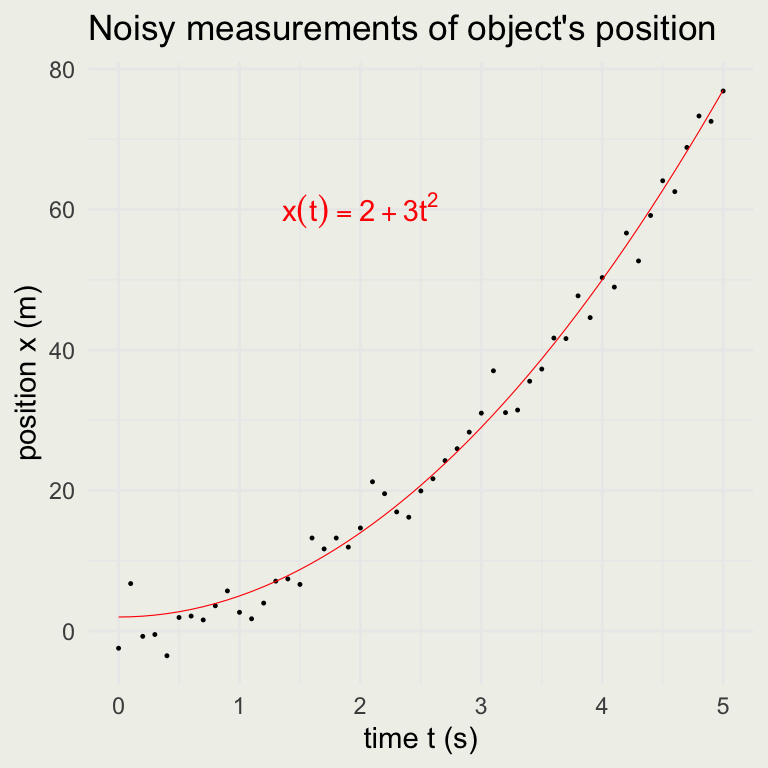
Example: Motion in a Straight Line
Suppose you have an experiment where you can measure the position of an object moving in a straight line every \(1/10\) of a second for 5 seconds. When you look at the graph of time versus position, it looks like this:
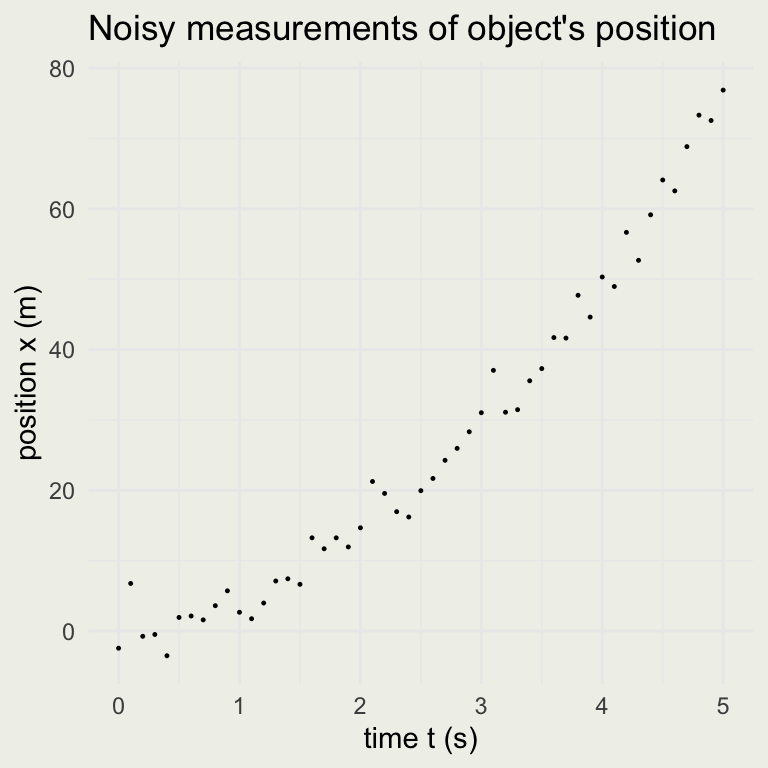
You guess that the function is quadratic in \(t\). If \(x\) is measured in meters, and \(t\) is in seconds, then \(a\) must have units of \(m\) and \(b\) must have units \(m/s^2\).
\[ x(t) = a + bt^2 \]
The statistical inference problem is to find plausible values of \(a\) and \(b\), given our noisy measurements and the assumption that the position function is quadratic. We will come back to how to do it later, but for now, assume that the most likely values were found to be \(a = 2\) and \(b = 3\).
We can now ask, what was the average velocity between \(1\) and \(4\) seconds? This is the same as the slope of the secant line:
\[ \bar{v} = \frac{\text{displacment} (m)}{\text{elapsed time} (s)} = \frac{\Delta x}{\Delta t} = \frac{x(4) - x(1)}{4-1} = \frac{50-5}{3} = 15 \text{ m/s} = 54 \text{ km/h} \]
Since we know that this is a line of the form \(x(t) = a + 15t\), that goes through the point \((t_1, x_1) = (1, 5)\), \(5 = a + 15\cdot1\) or \(a = -10\). The equation of the secant line is, therefore:
\[ x(t) = -10 + 15t \]
p <- ggplot(data.frame(t, x), aes(t, x))
p + geom_line(size = 0.2) +
geom_abline(slope = 15, intercept = -10, size = 0.2, color = 'red') +
geom_point(x = 1, y = 5, color = 'blue') +
geom_point(x = 4, y = 50, color = 'blue') +
xlab("time t (s)") + ylab("position x (m)") +
annotate("text", 3.7, 55, label = "(4, 50)") +
annotate("text", 1, 12, label = "(1, 5)") +
ggtitle("object's position function and the secant line")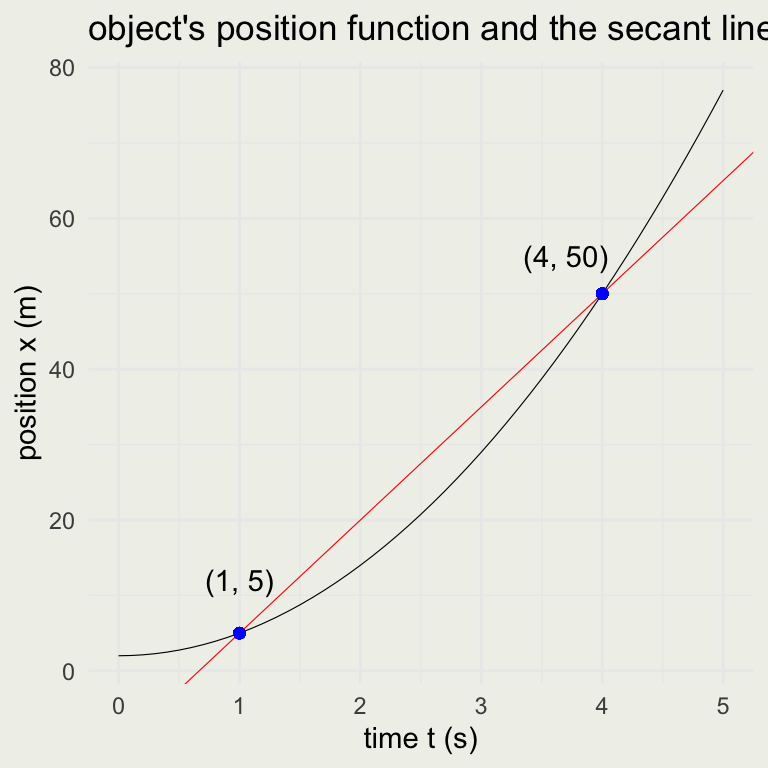
What if we wanted to know the speedometer reading at \(4\) seconds? In other words, we want to know the speed at that instant. This is where the limit comes in.
\[ v = \lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t} = \frac{dx}{dt} \]
The Derivative
- How do we compute this limit, which we wrote as \(dx/dt\)?
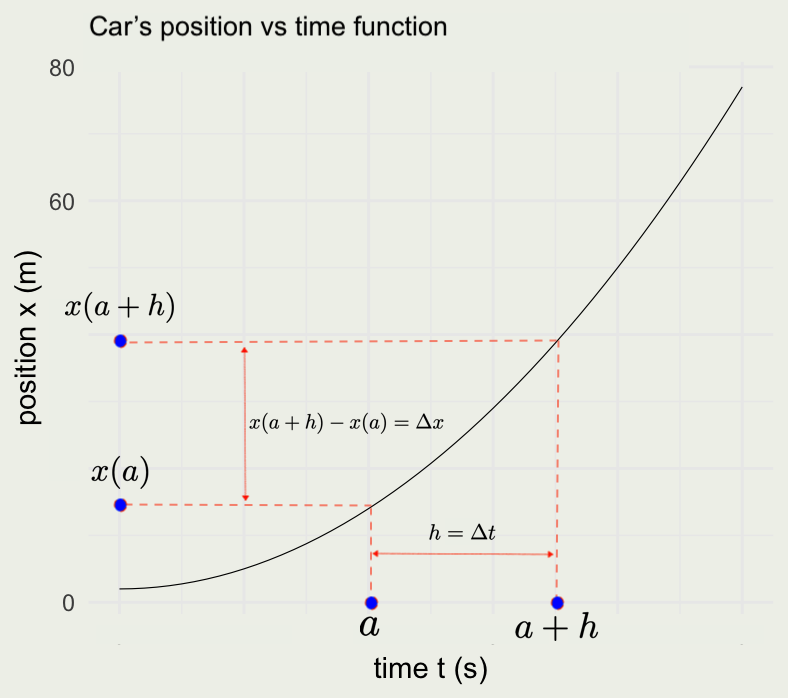
- We re-write the secant or average velocity equation in the following way:
\[ \begin{eqnarray} \bar v & = & \frac{x(a + h) - x(a)}{a + h - a} = \frac{x(a + h) - x(a)}{h} \\ v & = & \lim_{\Delta h \to 0} \frac{x(a + h) - x(a)}{h} \\ \end{eqnarray} \]
The Derivative
- Our original problem was to find the velocity at \(t = 4\) given our position function \(x(t) = 2 + 3t^2\).
\[ \begin{eqnarray} v & = & \lim_{\Delta h \to 0} \frac{x(a + h) - x(a)}{h} = \lim_{\Delta h \to 0} \frac{2 + 3(t + h)^2 - 2 - 3t^2}{h} = \\ & \lim_{\Delta h \to 0} & \frac{6ht + 3h^2}{h} = \lim_{\Delta h \to 0} (6t + 3h) = 6t \end{eqnarray} \]
At \(t = 4\), the speedometer was reading \(6 \cdot 4 = 24 \text{ m/s } = 86.4 \text{ km/h}\).
The velocity is the derivative of position with respect to time, and we can write:
\[ v(t) = \frac{dx}{dt} = 6t \]
The Derivative
- But what about acceleration?
- Acceleration is a change in velocity with respect to time or the second derivative of position:
\[ a(t) = \frac{dv}{dt} = \frac{d}{dt} \left( \frac{d x}{d t} \right) = \frac{d^2 x}{d t^2} \]
- To compute acceleration at \(t = 4\), we take the limit again, only this time with respect to the velocity function:
\[ a = \frac{dv}{dt} = \lim_{\Delta h \to 0} \frac{6(t + h) - 6t}{h} = \\ \lim_{\Delta h \to 0} \frac{6t + 6h - 6t}{h} = \lim_{\Delta h \to 0} 6 = 6 \]
- This function \(a(t) = 6\) does not depend on \(t\), and so acceleration is a constant \(6 \text{ m}/\text{s}^2\) at all values of \(t\) including \(t = 4\)
- It would be cumbersome to compute derivatives this way. Fortunately, we have shortcuts.
Rules of Differentiation
- We will state a few rules of differentiation without deriving them
\[ \begin{eqnarray} \frac{d}{dx}(c) & = & 0 \\ \frac{d}{dx}(x) & = & 1 \\ \frac{d}{dx}(x^n) & = & n x^{n-1} \\ \frac{d}{dx}[c f(x)] & = & c \frac{d}{dx}[f(x)] \\ \frac{d}{dx}[f(x) + g(x)] & = & \frac{d}{dx}f(x) + \frac{d}{dx}g(x) \\ \frac{d}{dx}(e^x) & = & e^x \\ \end{eqnarray} \]
Your Turn
- Suppose we have the following equations of motion:
\[ x(t) = 4 + 3t + 5t^2 \]
What is the object’s position at time zero and time 1 second?
What is the velocity at time zero?
What is the velocity and acceleration at 5 seconds?
Product Rule and Chain Rule
- Product and chain rules help us differentiate products and compositions of functions, respectively.
- Intuition for those can be found in the Essense of Calculus video.
- We will state them here without derivation. Product rule: Right d left, Left d right.
\[ \frac{d}{dx}[f(x) g(x)] = f(x) \frac{d}{dx}[g(x)] + g(x)\frac{d}{dx}[f(x)] \]
- If \(F = f \circ g\), in that \(F(x)= f(g(x))\):
\[ F'(x) = f'(g(x))g'(x) \]
Example of a Product Rule
- Suppose we wanted to compute the derivative of \(x(t) = \sin(t) \cos(t)\)
\[ \begin{eqnarray} \frac{d}{dt}(\sin(t) \cos(t)) & = & \\ \sin(t)\frac{d}{dt}[\cos(t)] + \cos(t)\frac{d}{dt}[\sin(t)] & = & \\ \sin(t) (-\sin(t)) + \cos(t)\cos(t) & = & \\ \cos^2(t) - \sin^2(t) \end{eqnarray} \]
Approximating Derivatives
library(ggplot2)
library(dplyr)
n <- 100
t <- seq(0, pi, length = n)
x <- sin(t) * cos(t)
dxdt <- cos(t)^2 - sin(t)^2
d <- tibble(t, x, dxdt)
p <- ggplot(d, aes(t, x))
p + geom_line() + geom_line(aes(y = dxdt), col = 'red')
# approximate the derivative
s <- pi / (n - 1) # choose the same step s as the increment in the t sequence
all.equal(s, diff(t)[1]) # check that the above statement is true[1] TRUEappr_dxdt <- diff(x)/s # derivative ≈ rise / run
d <- d |>
mutate(appr_dxdt = c(NA, appr_dxdt))
p <- ggplot(d, aes(t, x))
p + geom_line() + geom_line(aes(y = dxdt), col = 'red') +
geom_line(aes(y = appr_dxdt), col = 'blue', linewidth = 5, alpha = 1/5)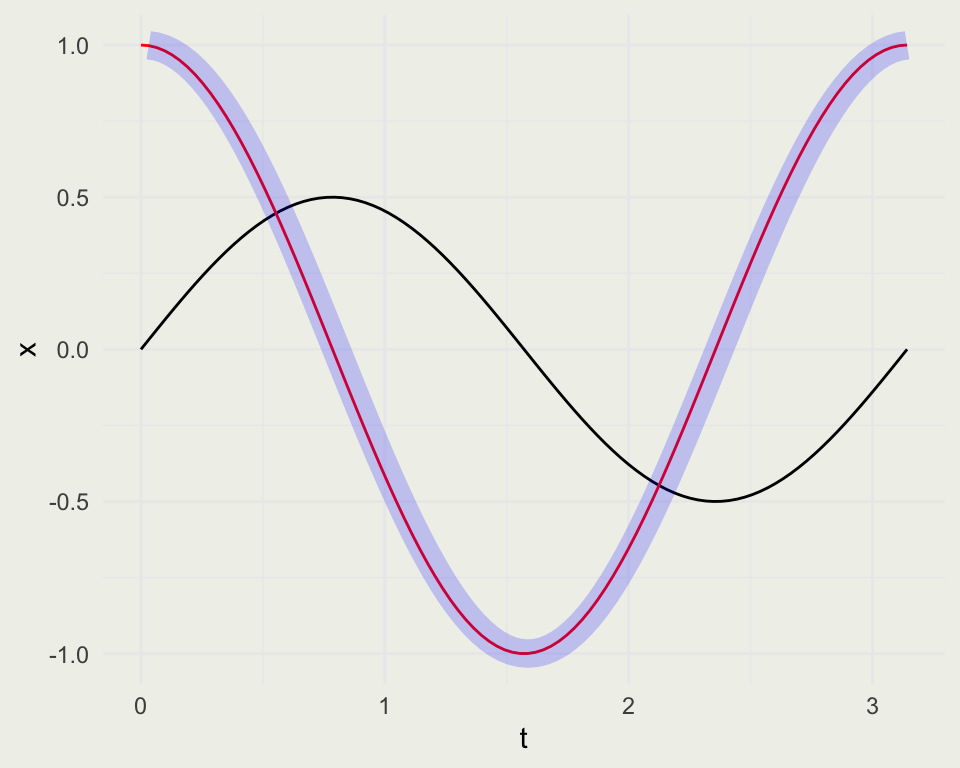
Examples of the Chain Rule
What is the derivative of \(\sin(x^2)\)? It is \(2x \cos(x^2)\)
Your turn: \[ \frac{d}{dx} \left( e^{\cos(x) x^2} \right ) = \]
Homework
- A particle is moving in a counter-clockwise uniform circular motion according to the following equations:
\[ x(t) = R \cos(\omega t) \\ y(t) = R \sin(\omega t) \]
- Where \(\omega\) is called angular frequency (radians per unit of time) and \(R\) is the radius of rotation. The full cycle is achieved when \(T = 2 \pi/ \omega\)
- Create two functions that take \(R\), \(t\), and \(\omega\) as parameters
- Create a vector \(t\) of length 100 that achieves one full rotation
- Plot the \(x\) position against \(t\) and the \(y\) position against \(t\) on the same graph
- Now plot \(x\) against \(y\). Do the plots make sense?
- Create 4 more functions: 2 for velocity (in x and y direction) and 2 for acceleration
- Plot the velocity against the position (say in the x direction) and the velocity against acceleration
- What have you learned?