SMaC: Statistics, Math, and Computing

APSTA-GE 2006: Applied Statistics for Social Science Research

Eric.Novik@nyu.edu | Summer 2026 | Session 7

Session 7 Outline

  • Statistical inference
  • Sampling distribution
  • Standard errors
  • Confidence intervals
  • Degrees of freedom and t distribution
  • Bias and uncertainty
  • Statistical significance

The material for this session is based on Chapter 4 of the Regression and Other Stories by Gelman et al.

\[ \DeclareMathOperator{\E}{\mathbb{E}} \DeclareMathOperator{\P}{\mathbb{P}} \DeclareMathOperator{\V}{\mathbb{V}} \DeclareMathOperator{\L}{\mathscr{L}} \DeclareMathOperator{\I}{\text{I}} \]

Introduction to Statistical Inference

  • Statistical Inference: A process of learning from noisy measurements
  • Key Challenges:
    • Generalizing from a sample to the population of interest
    • Learning what would have happened under a different treatment
    • Understanding the relationship between the measurement and the estimand

Measurement Error Models

  • We are trying to estimate the parameters of some data-generating process
  • For the Moon drop, the distance marks \(x_i\) are fixed and the stopwatch times are noisy:

\[ t_i=\alpha+\sqrt{\frac{2x_i}{g}}+\epsilon_i =\alpha+\beta\sqrt{x_i}+\epsilon_i, \qquad \beta=\sqrt{\frac{2}{g}}. \]

  • Here \(\alpha\) is a constant timing delay and \(\epsilon_i\) is random timing error
  • Other measurement mechanisms may require different additive or multiplicative error models

Sampling Distribution

  • A generative model describes how repeated datasets could arise under fixed assumptions
  • “The sampling distribution is the set of possible datasets that could have been observed if the data collection process had been re-done, along with the probabilities of these possible values.” Ch-4 ROS, Gelman, Hill, Vehtari
  • It depends on the sampling design, treatment-assignment mechanism, and measurement process
  • Examples
    • In a simple random sample of size \(n\) from a population of size \(N\), every subset of \(n\) people has the same probability of being selected
    • For the Moon drop, fix \(\alpha\), \(\beta\), and the marks \(x_i\), then draw timing errors \(\epsilon_i\) and form \(t_i=\alpha+\beta\sqrt{x_i}+\epsilon_i\)
    • We can write code to generate observations from this process, as we did for the Moon drop

Standard Errors

  • Standard error is the estimated standard deviation of the estimate
  • It provides a measure of uncertainty around the estimate
  • Holding the data-generating process fixed, standard errors typically decrease as sample size increases
  • For the mean of \(n\) independent observations with population sd \(\sigma\): \(\text{se}(\bar{x})=\frac{\sigma}{\sqrt{n}}\)
set.seed(1)
n <- 100; mu <- 5; sigma <- 1.5
x <- rnorm(n, mean = mu, sd = sigma)
x_bar <- mean(x); round(x_bar, 2)
[1] 5.16
se <- sigma/sqrt(n)
print(se)
[1] 0.15

Estimating the Standard Error

  • If \(\sigma\) is unknown, estimate it from the sample: \(s = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2}\)
  • Then \(\widehat{\text{se}}(\bar{x})=s/\sqrt{n}\)
sd(x) |> round(2)
[1] 1.35
sd_s <- sqrt(sum((x - x_bar)^2) / (n - 1))
print(sd_s |> round(2))
[1] 1.35
se_s <- sd_s/sqrt(n)
print(se_s |> round(2))
[1] 0.13

Confidence Intervals

  • For a given sampling distribution, a confidence interval provides a range of parameter values consistent with the data
  • If \(\hat{\theta}\) is approximately Normal and its standard error is estimated well, repeated intervals \(\hat{\theta} \pm 1.96\cdot\text{se}\) cover the true \(\theta\) about 95% of the time

Confidence Intervals for Proportions

  • In surveys, we are often interested in estimating the standard error of the proportion
  • Suppose we want to estimate the proportion of the US population that supports same-sex marriage
  • Say you randomly survey \(n = 500\) from the population, and \(y = 355\) people respond yes (*)
  • The estimate of the proportion is \(\hat{\theta} = y/n\) with the \(\text{se} = \sqrt{\hat{\theta}(1 -\hat{\theta})/n }\)
n <- 500
y <- 355
theta_hat <- y/n
theta_hat |> round(2)
[1] 0.71
se <- sqrt(theta_hat * (1 - theta_hat) / n)
se |> round(2)
[1] 0.02
theta_hat + 2*se |> round(2)
[1] 0.75
theta_hat - 2*se |> round(2)
[1] 0.67
ci_95 <- theta_hat + qnorm(c(0.025, 0.975)) * se
ci_95 |> round(2)
[1] 0.67 0.75

(*) A May 2023 Gallup poll found that 71% of Americans thought same-sex marriage should be legally recognized

Your Turn

Assume the conservative value \(p=0.5\). In a national survey, how large must \(n\) be so that \(\text{se}(\hat p)\) is at most:

  • 3 percentage points?
  • 1 percentage point?

Standard Error for Differences

  • For two independent estimates, variances add:

\[ \text{se}_{\text{diff}} = \sqrt{\text{se}_1^2 + \text{se}_2^2} \]

  • Your turn: Assume two independent, equally sized groups, \(p_1=p_2=0.5\), and \(n\) is the total sample size. How large must \(n\) be so that \(\text{se}(\hat p_1-\hat p_2)\leq 0.03\)?

Moon Drop: How Many Drops?

Each drop gives 20 noisy time readings at fixed distance marks, and each drop costs oxygen. Here we omit the delay term and impose the physical constraint \(t(0)=0\). We repeatedly fit \(t=\beta\sqrt{x}+\varepsilon\) through the origin and transform \(\hat g=2/\hat\beta^2\).

set.seed(1)
g_true <- 1.625
timing_sd <- 0.10                         # random timing noise, seconds
reps <- 500
marks <- seq(5, 100, by = 5)              # fixed marks every 5 m
sqrt_marks <- sqrt(marks)
beta_true <- sqrt(2 / g_true)

se_ghat <- function(n_drops) {
  z <- rep(sqrt_marks, n_drops)            # fixed design values
  g_hat <- replicate(reps, {
    t_obs <- beta_true * z +
      rnorm(length(z), 0, timing_sd)
    beta_hat <- coef(lm(t_obs ~ 0 + z))[["z"]]
    2 / beta_hat^2
  })
  sd(g_hat)                                # empirical SE of g_hat
}

Moon Drop: Simulation Results

drops <- c(1, 2, 3, 5, 10, 12, 15, 20, 40)
se_g <- purrr::map_dbl(drops, se_ghat)
moon_drop_results <- data.frame(
  drops = drops,
  readings = drops * 20,
  se_g = round(se_g, 4),
  half_width = round(1.96 * se_g, 4)
)
moon_drop_results
  drops readings   se_g half_width
1     1       20 0.0089     0.0175
2     2       40 0.0061     0.0119
3     3       60 0.0054     0.0107
4     5      100 0.0040     0.0079
5    10      200 0.0029     0.0057
6    12      240 0.0026     0.0052
7    15      300 0.0025     0.0048
8    20      400 0.0020     0.0039
9    40      800 0.0014     0.0027
  • Rows: each row summarizes 500 simulated repetitions; readings is 20 times drops
  • se_g: empirical standard deviation of the 500 \(\hat g\) values
  • half_width: \(1.96\,\text{se}_g\), an approximate 95% margin; smaller is more precise
  • Precision targets: one decimal requires half_width \(\leq0.05\) (half of 0.1); two decimals requires half_width \(\leq0.005\) (half of 0.01)
  • Reading the table: one drop has \(0.0175<0.05\); 12 drops have \(0.0052>0.005\), while 15 drops have \(0.0048<0.005\)

Computer Demo: Computing CIs

# Generate fake data
p <- 0.3
n <- 20
data <- rbinom(1, n, p)
print(data)

# Estimate proportion and calculate confidence interval
p_hat <- data / n
se <- sqrt(p_hat * (1 - p_hat) / n)
ci <- p_hat + c(-2, 2) * se
print(ci)

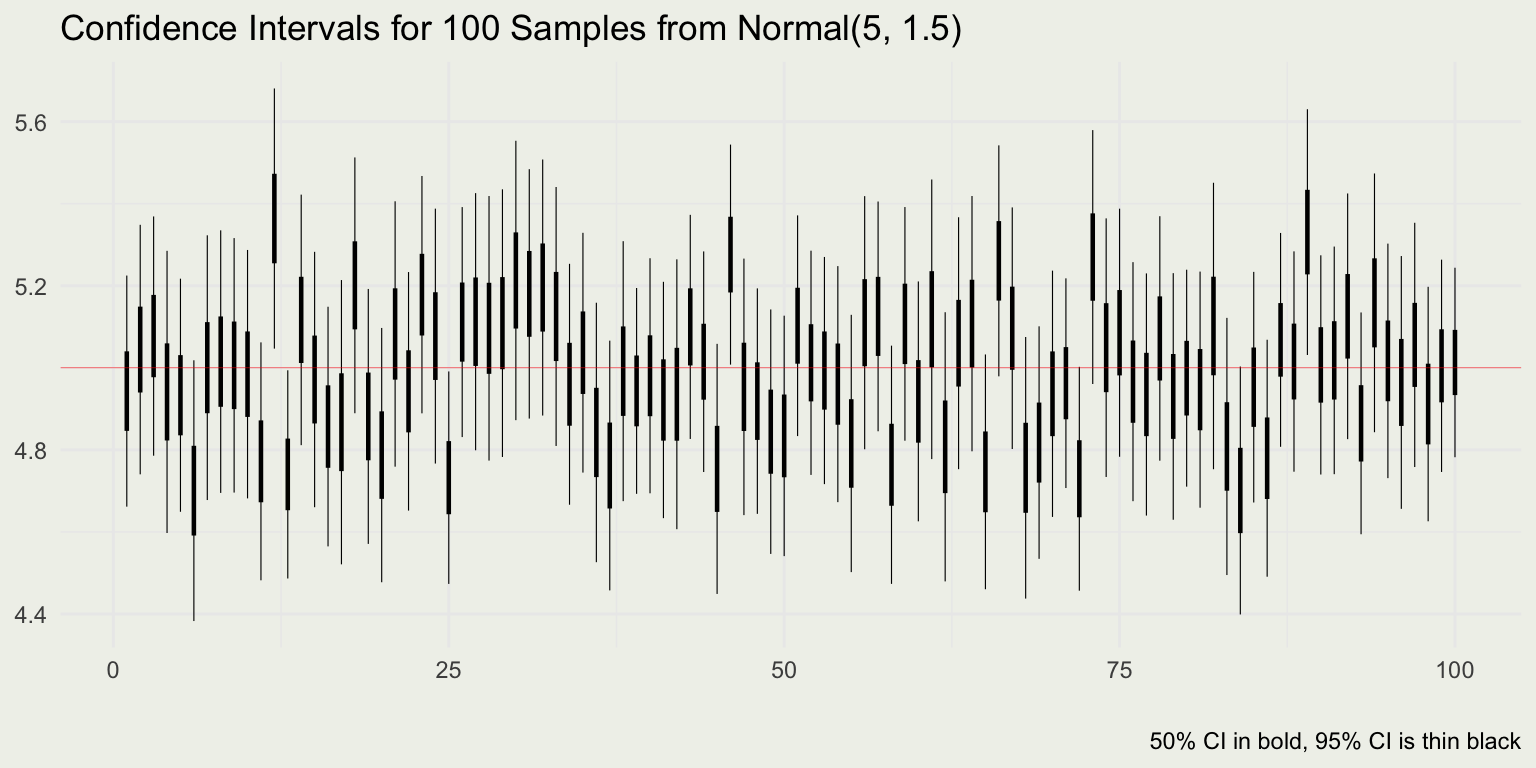
# Put it in a loop
reps <- 100
for (i in 1:reps) {
  data <- rbinom(1, n, p)
  p_hat <- data / n
  se <- sqrt(p_hat * (1 - p_hat) / n)
  ci <- p_hat + c(-2, 2) * se
  print(ci)
}

Computer Demo: Proportions, Means, and Differences of Means

# Read data from here:  https://github.com/avehtari/ROS-Examples
library("foreign")
library("dplyr")
pew_pre <- read.dta(
  paste0(
    "https://raw.githubusercontent.com/avehtari/",
    "ROS-Examples/master/Pew/data/",
    "pew_research_center_june_elect_wknd_data.dta"
  )
)
pew_pre <- pew_pre |> select(c("age", "regicert")) %>%
  na.omit() |> filter(age != 99)
n <- nrow(pew_pre)

# Estimate a proportion (certain to have registered for voting?)
registered <- ifelse(pew_pre$regicert == "absolutely certain", 1, 0)
p_hat <- mean(registered)
se_hat <- sqrt((p_hat * (1 - p_hat)) / n)
round(p_hat + c(-2, 2) * se_hat, 4) # ci

# Estimate an average (mean age)
age <- pew_pre$age
y_hat <- mean(age)
se_hat <- sd(age) / sqrt(n)
round(y_hat + c(-2, 2) * se_hat, 4) # ci

# Estimate a difference of means
age2 <- age[registered == 1]
age1 <- age[registered == 0]
y_2_hat <- mean(age2)
se_2_hat <- sd(age2) / sqrt(length(age2))
y_1_hat <- mean(age1)
se_1_hat <- sd(age1) / sqrt(length(age1))
diff_hat <- y_2_hat - y_1_hat
se_diff_hat <- sqrt(se_1_hat ^ 2 + se_2_hat ^ 2)
round(diff_hat + c(-2, 2) * se_diff_hat, 4) # ci

Degrees of Freedom

  • Degrees of freedom count independent pieces of information remaining after accounting for constraints or fitted parameters
  • In a full-rank linear model with \(n\) observations and \(p\) fitted coefficients, the residual degrees of freedom are \(n-p\)
  • For a sample variance, the deviations from \(\bar{x}\) must sum to zero, leaving \(n-1\) degrees of freedom

Normal and t Distributions

  • Student’s t distribution has a degrees-of-freedom parameter; with few degrees of freedom, it has heavier tails than the Normal distribution

Confidence Intervals from the t Distribution

  • For i.i.d. Normal data with unknown variance, \((\bar X-\mu)/(s/\sqrt n)\) follows \(t_{n-1}\)
  • It is the t reference distribution—not the standard error itself—that has \(n-1\) degrees of freedom
  • Example: five dart distances from the bull’s eye, in cm (dartboard radius \(\approx 23\) cm)
# Distance from the bull's eye in cm
data <- c(8, 6, 10, 5, 18)

# Calculate the sample mean
mean_data <- mean(data)

# Calculate the standard error of the mean
se_mean <- sd(data) / sqrt(length(data))

# Degrees of freedom
df <- length(data) - 1

# Calculate the 95% and 50% confidence interval
ci_95 <- mean_data + qt(c(0.025, 0.975), df) * se_mean
ci_50 <- mean_data + qt(c(0.25, 0.75), df) * se_mean

# Output the results
mean_data |> round(2)
[1] 9.4
se_mean |> round(2)
[1] 2.32
ci_95 |> round(2)
[1]  2.97 15.83
ci_50 |> round(2)
[1]  7.69 11.11

Bias and Uncertainty

  • There is a lot more to it than what is in the following standard picture
  • Discuss among yourselves what are the potential sources of bias

Statistical Significance

  • Comes up in NHST: Null Hypothesis Significance Testing
  • Bad decision filter: if p-value is less than 0.05 (relative to some Null), the results can be trusted, otherwise they are likely noise
  • For a test statistic \(T\) where larger values are more extreme under \(H_0\):

\[ \text{p-value}(y) = \P\!\left(T(Y_\text{rep}) \geq T(y) \mid H_0\right) \]

  • Often, estimates are labeled not significant when they are within roughly 2 SEs of the null value (commonly zero for a coefficient); selecting models this way is also problematic

Some Problems with Statistical Significance