SMaC: Statistics, Math, and Computing

APSTA-GE 2006: Applied Statistics for Social Science Research

Eric.Novik@nyu.edu | Summer 2025 | Session 8

Session 8 Outline

  • Statistical analysis workflow
  • Simulating data for simple regression
  • Binary predictor in a regression
  • Adding continuous predictor
  • Combining binary and continuous predictors
  • Interpreting coefficients
  • Adding interactions
  • Uncertainty and predictions
  • Assumptions of the regression analysis
  • Regression modeling advice

\[ \DeclareMathOperator{\E}{\mathbb{E}} \DeclareMathOperator{\P}{\mathbb{P}} \DeclareMathOperator{\V}{\mathbb{V}} \DeclareMathOperator{\L}{\mathscr{L}} \DeclareMathOperator{\I}{\text{I}} \]

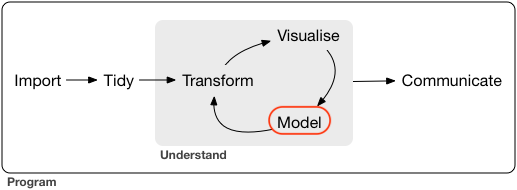
Analysis Workflow

  • Following is a high-level, end-to-end view from “R for Data Science” by Wickham and Grolemund

Some Notation

  • Observed data \(y\)
  • Unobserved but observable data \(\widetilde{y}\)
  • Unobservable parameters \(\theta\)
  • Covariates \(X\)
  • Prior distribution \(f(\theta)\) (for Bayesian inference)
  • Data model or sampling distribution (as a function of y) \(f(y \mid \theta, X)\)
  • Likelihood (as a function of \(\theta\)), \(f(y \mid \theta, X)\), sometimes written as \(\mathcal{L}(\theta \mid y, X)\)
  • Maximum likelihood estimate (MLE): \(\hat{\theta} = \underset{\theta}{\text{argmax}} \, \mathcal{L}(\theta \mid y, X)\) (for Frequentist inference)
  • Posterior distribution \(f(\theta \mid y, X)\) (for Bayesian inference)

Bayes vs Frequentist Inference

  • Estimation is the process of figuring out the unknowns, i.e., unobserved quantities
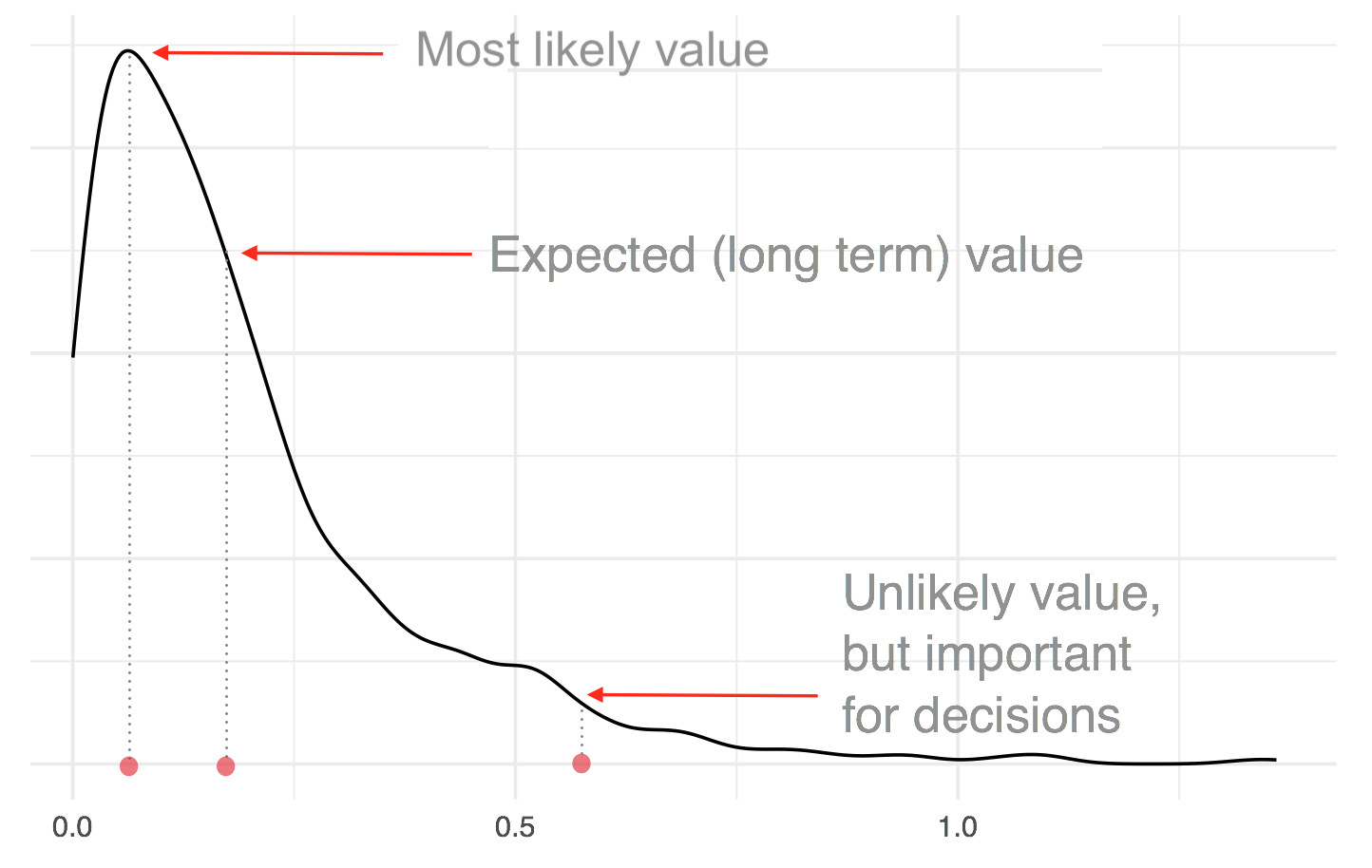
  • In frequentist inference, the problem is framed in terms of the most likely value(s) of \(\theta\)
  • Bayesians want to characterize the whole distribution, a much more ambitious goal
  • Suppose we want to characterize the following function, which represents some distribution of the unknown parameter:

Basic Regression Setup

  • There are lots of possible ways to set up a regression
  • One predictor: \(y = a + bx + \epsilon\)
  • Multiple predictors: \(y = b_0 + b_1x_1 + b_2x_2 + \cdots + b_nx_n + \epsilon\), which we can write as \(y = X\beta + \epsilon\)
  • Models with interactions: \(y = b_0 + b_1x_1 + b_2x_2 + b_3x_1x_2 + \epsilon\)
  • Non-linear models like: \(\log(y) = a + b\log(x) + \epsilon\)
  • Generalized Linear Models (GLMs), which can, for example, fit binary data, categorical data, and so on
  • Nonparametric models that are popular in Machine Learning that can learn flexible, functional forms between \(y\) and \(X\)
  • The latter is not a panacea — if you have a good or good enough functional form, predictions will generally be better and the model will generalize better

Most of the material in this section comes from Regression and Other Stories by Gelman et al. 

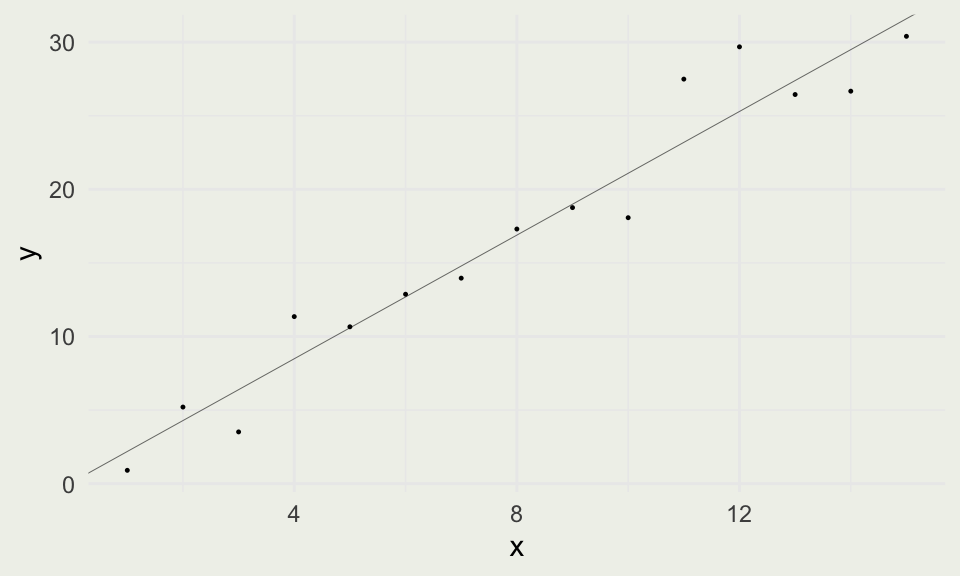
Simulating a Simple Regression

  • Fitting simulated data is a good start for an analysis
library(rstanarm)
n <- 15; x <- 1:n
a <- 0.5
b <- 2
sigma <- 3
y <- a + b*x + rnorm(n, mean = 0, sd = sigma) # or sigma * rnorm(n)
data <- data.frame(x, y)
fit1 <- stan_glm(y ~ x, data = data, refresh = 0) 
print(fit1)
stan_glm
 family:       gaussian [identity]
 formula:      y ~ x
 observations: 15
 predictors:   2
------
            Median MAD_SD
(Intercept) 0.1    1.4   
x           2.1    0.2   

Auxiliary parameter(s):
      Median MAD_SD
sigma 2.6    0.5   

------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg

Simulating a Simple Regression

  • We extract our betas using the coef() R function
a_hat <- coef(fit1)[1]
b_hat <- coef(fit1)[2]
p <- ggplot(aes(x, y), data = data)
p + geom_point(size = 0.2) + geom_abline(intercept = a_hat, slope = b_hat, linewidth = 0.1)

KidIQ Dataset

  • Data from a survey of adult American women and their children (a subsample from the National Longitudinal Survey of Youth).
knitr::kable(rstanarm::kidiq[1:8, ])
kid_score mom_hs mom_iq mom_age
65 1 121.11753 27
98 1 89.36188 25
85 1 115.44316 27
83 1 99.44964 25
115 1 92.74571 27
98 0 107.90184 18
69 1 138.89311 20
106 1 125.14512 23

Single Binary Predictor

fit2 <- stan_glm(kid_score ~ mom_hs, data = kidiq, refresh = 0) 
print(fit2)
stan_glm
 family:       gaussian [identity]
 formula:      kid_score ~ mom_hs
 observations: 434
 predictors:   2
------
            Median MAD_SD
(Intercept) 77.6    2.0  
mom_hs      11.8    2.4  

Auxiliary parameter(s):
      Median MAD_SD
sigma 19.9    0.7  

------
* For help interpreting the printed output see ?print.stanreg
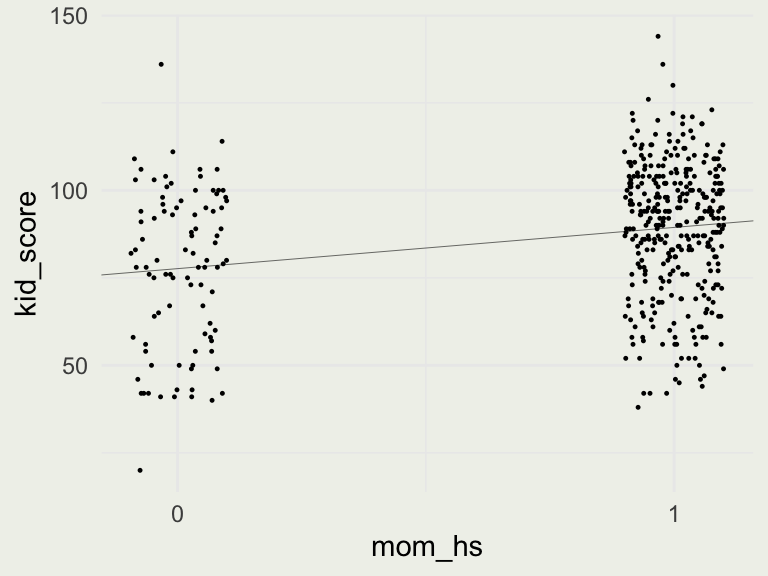
* For info on the priors used see ?prior_summary.stanreg
  • Our model is \(\text{kid_score} = 78 + 12 \cdot \text{mom_hs} + \epsilon\)
  • What is the average IQ of kids whose mothers did not complete high school? (in this dataset)
  • What is the average IQ of kids whose mothers completed high school?
  • Did high school cause the IQ change?

Single Binary Predictor

p <- ggplot(aes(mom_hs, kid_score), data = kidiq)
p + geom_jitter(height = 0, width = 0.1, size = 0.2) +
  geom_abline(intercept = coef(fit2)[1], slope = coef(fit2)[2], linewidth = 0.1) +
  scale_x_continuous(breaks = c(0, 1))

Single Continous Predictor

fit3 <- stan_glm(kid_score ~ mom_iq, data = kidiq, refresh = 0) 
print(fit3)
stan_glm
 family:       gaussian [identity]
 formula:      kid_score ~ mom_iq
 observations: 434
 predictors:   2
------
            Median MAD_SD
(Intercept) 26.0    6.1  
mom_iq       0.6    0.1  

Auxiliary parameter(s):
      Median MAD_SD
sigma 18.3    0.6  

------
* For help interpreting the printed output see ?print.stanreg
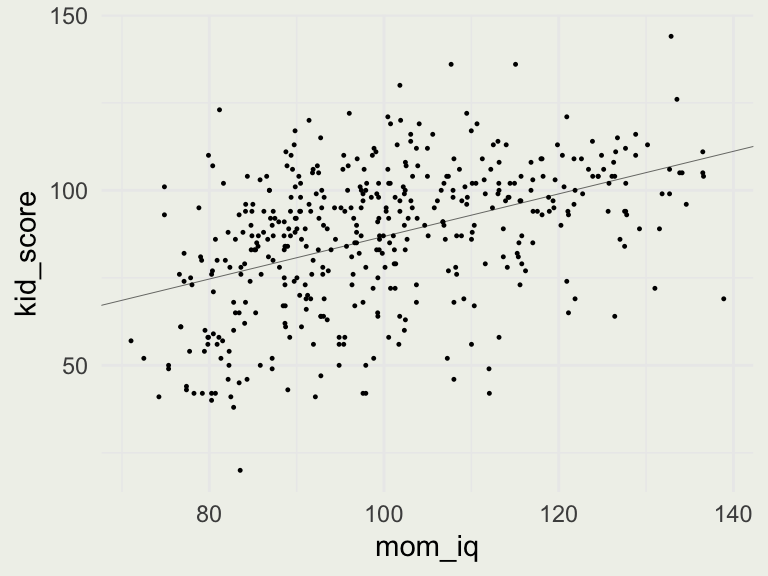
* For info on the priors used see ?prior_summary.stanreg
  • Our model is \(\text{kid_score} = 26 + 0.6 \cdot \text{mom_iq}+ \epsilon\)
  • How much do kids’ scores improve when maternal IQ differs by 10 points?
  • What is the meaning of the intercepts = 26 here?

Simple Transformations

  • We will create a new variable called mom_iq_c, which stands for centered
  • The transformation: \(\text{mom_iq_c}_i = \text{mom_iq}_i - \overline{\text{mom_iq}}\)
kidiq <- kidiq |>
  mutate(mom_iq_c = mom_iq - mean(mom_iq))
fit4 <- stan_glm(kid_score ~ mom_iq_c, data = kidiq, refresh = 0) 
print(fit4)
stan_glm
 family:       gaussian [identity]
 formula:      kid_score ~ mom_iq_c
 observations: 434
 predictors:   2
------
            Median MAD_SD
(Intercept) 86.8    0.9  
mom_iq_c     0.6    0.1  

Auxiliary parameter(s):
      Median MAD_SD
sigma 18.3    0.6  

------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg
  • Our model is \(\text{kid_score} = 87 + 0.6 \cdot \text{mom_iq_c}+ \epsilon\)
  • What is the meaning of the intercepts in this model?

Single Continous Predictor

p <- ggplot(aes(mom_iq, kid_score), data = kidiq)
p + geom_point(size = 0.2) +
  geom_abline(intercept = coef(fit3)[1], slope = coef(fit3)[2], linewidth = 0.1)

Combining the Predictors

fit5 <- stan_glm(kid_score ~ mom_hs + mom_iq_c, data = kidiq, refresh = 0)
print(fit5)
stan_glm
 family:       gaussian [identity]
 formula:      kid_score ~ mom_hs + mom_iq_c
 observations: 434
 predictors:   3
------
            Median MAD_SD
(Intercept) 82.2    1.9  
mom_hs       6.0    2.2  
mom_iq_c     0.6    0.1  

Auxiliary parameter(s):
      Median MAD_SD
sigma 18.2    0.6  

------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg
  • Our model is now: \(\text{kid_score} = 82 + 6 \cdot \text{mom_hs} + 0.6 \cdot \text{mom_iq_c}+ \epsilon\)
  • Write down the interpretation of each coefficient

Combining the Predictors

stan_glm
 family:       gaussian [identity]
 formula:      kid_score ~ mom_hs + mom_iq
 observations: 434
 predictors:   3
------
            Median MAD_SD
(Intercept) 25.8    5.9  
mom_hs       6.0    2.3  
mom_iq       0.6    0.1  

Auxiliary parameter(s):
      Median MAD_SD
sigma 18.2    0.6  

------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg
  • Our model is: \(\text{kid_score} = 26 + 6 \cdot \text{mom_hs} + 0.6 \cdot \text{mom_iq}+ \epsilon\)
  • For moms that did not complete high school, the line \(y = 26 + 0.6 \cdot \text{mom_iq}\)
  • For moms that did: \(\text{kid_score} = 26 + 6 \cdot 1 + 0.6 \cdot \text{mom_iq} = 32 + 0.6 \cdot \text{mom_iq}\)

Visualizing the Fit With Two Predictors

p <- ggplot(aes(mom_iq, kid_score), data = kidiq)
p + geom_point(aes(color = as.factor(mom_hs)), size = 0.2) +
  labs(color = "Mom HS") +
  geom_abline(intercept = coef(fit6)[1], slope = coef(fit6)[3], linewidth = 0.1, color = 'red') +
  geom_abline(intercept = coef(fit6)[1] + coef(fit6)[2], slope = coef(fit6)[3], linewidth = 0.1, color = 'blue')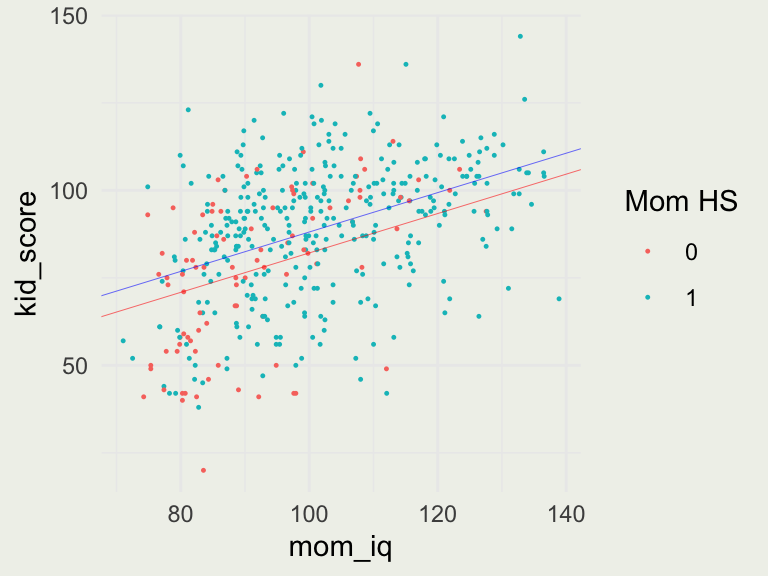

Adding Interactions

  • In the previous model, we forced the slopes of mothers who completed and did not complete high school to be the same — the only difference was the intercept
  • To allow the slopes to vary, we include an interaction term
stan_glm
 family:       gaussian [identity]
 formula:      kid_score ~ mom_hs + mom_iq + mom_hs:mom_iq
 observations: 434
 predictors:   4
------
              Median MAD_SD
(Intercept)   -10.6   13.7 
mom_hs         50.2   15.1 
mom_iq          1.0    0.1 
mom_hs:mom_iq  -0.5    0.2 

Auxiliary parameter(s):
      Median MAD_SD
sigma 18.0    0.6  

------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg
  • Our model is: \(\text{kid_score} = -10 + 49 \cdot \text{mom_hs} + 1 \cdot \text{mom_iq} - 0.5 \cdot \text{mom_hs} \cdot \text{mom_iq} + \epsilon\)
  • To figure out the slopes, we consider two cases
  • For \(\text{mom_hs} = 0\), the line is: \(\text{kid_score} = -10 + 1 \cdot \text{mom_iq}\)
  • For \(\text{mom_hs} = 1\), the line is: \(\text{kid_score} = -10 + 49 \cdot 1 + 1 \cdot \text{mom_iq} - 0.5 \cdot 1 \cdot \text{mom_iq} = 39 + 0.5\cdot \text{mom_iq}\)

Visualizing Interactions

p <- ggplot(aes(mom_iq, kid_score), data = kidiq)
p + geom_point(aes(color = as.factor(mom_hs)), size = 0.2) +
  labs(color = "Mom HS") +
  geom_abline(intercept = coef(fit7)[1], slope = coef(fit7)[3], linewidth = 0.1, color = 'red') +
  geom_abline(intercept = coef(fit7)[1] + coef(fit7)[2], slope = coef(fit7)[3] + coef(fit7)[4], linewidth = 0.1, color = 'blue')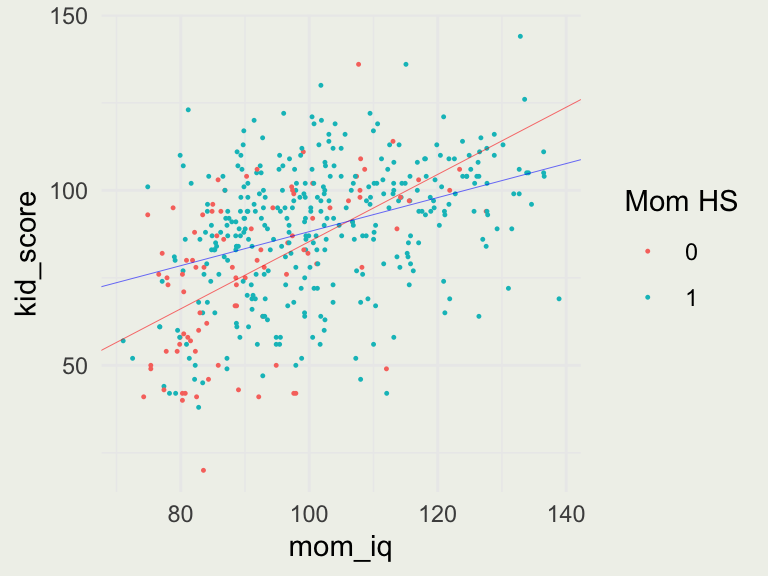

Interpreting Coefficients in Complex Non-Linear Models

  • Models that have many parameters, many interactions, and are non-linear are difficult to interpret by looking at parameters marginally (i.e., one at a time)
  • For this reason, we typically rely on assessing how changes to model inputs affect model predictions, not the impact of each parameter
  • Predictions take all the parameter values and their interactions into account

Uncertainty and Prediction

  • We return to our simple linear regression model: \(\text{kid_score} = 26 + 0.6 \cdot \text{mom_iq}+ \epsilon\)
  • We can extract the simulations of all plausible parameter values (called a posterior distribution in Bayesian analysis)
post <- as.matrix(fit3)
dim(post)
[1] 4000    3
knitr::kable(post[1:5, ])
(Intercept) mom_iq sigma
31.77474 0.5396861 18.28899
27.21061 0.5917098 18.20332
27.27470 0.5942835 18.29135
26.54087 0.6114706 18.79476
25.46339 0.6054314 17.86559

Uncertainty and Prediction

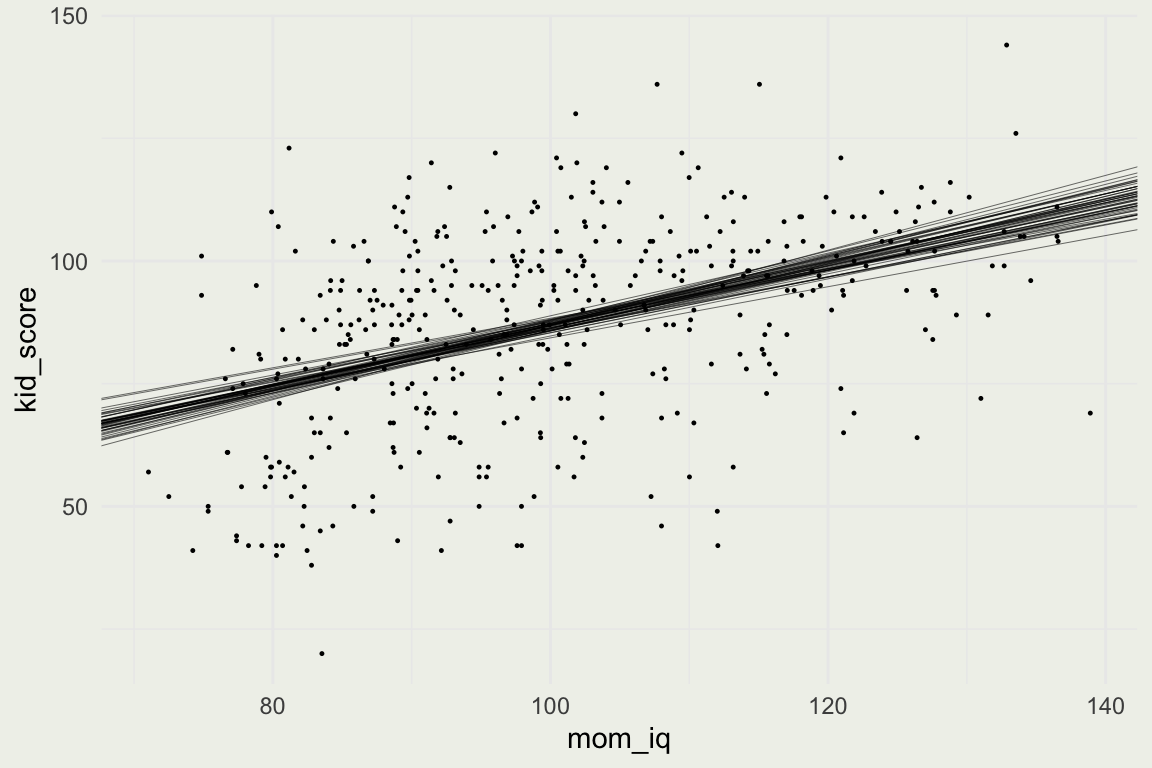
  • Using these simulations we display 50 plausible regression lines
post <- as.data.frame(fit3)
post_sub <- post[sample(1:nrow(post), 50), ]
p <- ggplot(aes(mom_iq, kid_score), data = kidiq)
p + geom_point(size = 0.2) + 
  geom_abline(aes(intercept = `(Intercept)`, slope = mom_iq), 
              linewidth = 0.1,
              data = post_sub)

Uncertainty and Prediction

  • We can compute inferential uncertainty in all the parameters directly
  • We can also compute event probabilities
post <- as.matrix(fit3)
# median
apply(post, 2, median)
(Intercept)      mom_iq       sigma 
 26.0236767   0.6078977  18.2714868 
apply(post, 2, mad)
(Intercept)      mom_iq       sigma 
 6.10031655  0.06062729  0.61543505 
# 50% uncertainty estimate
apply(post, 2, quantile, probs = c(0.25, 0.75))
     parameters
      (Intercept)    mom_iq    sigma
  25%    21.75756 0.5681001 17.86710
  75%    30.06156 0.6504483 18.69458
# 90% uncertainty estimate
apply(post, 2, quantile, probs = c(0.05, 0.95))
     parameters
      (Intercept)    mom_iq    sigma
  5%     15.72707 0.5106528 17.32535
  95%    35.77134 0.7095889 19.33193
# What is the probability that the coefficient of mom_iq is > 0.6
mean(post[, "mom_iq"] > 0.6) |> round(2)
[1] 0.55

Types of Prediction

  • Point prediction: \(\hat{a} + \hat{b}x^{\text{new}}\) — predicting expected average \(y\) — don’t recommend
  • Linear predictor with uncertainty in \(a\) and \(b\): \(a + bx^{\text{new}}\) — predicting uncertainty around the expexted average value of \(y\) — typically used to assess treatment effect
  • Predictive distribution: \(a + bx^{\text{new}} + \epsilon\) — predictive uncertainty around a new \(y\) — used to predict for a new individual (not ATT)

Prediction in RStanArm

  • We observe a new kid whose mom’s IQ = 120
  • Point prediction is shown in Red, 90% uncertainty around the average kid score in Blue, and 90% predictive uncertainty for a new kid is in Yellow.
mom120 <- data.frame(mom_iq = 120)
(point_pred <- predict(fit3, newdata = mom120))
      1 
98.9816 
lin_pred <- posterior_linpred(fit3, 
                              newdata = mom120)
post_pred <- posterior_predict(fit3, 
                               newdata = mom120)
(lp_range <- quantile(lin_pred, 
                      probs = c(0.05, 0.95)))
      5%      95% 
 96.5370 101.4359 
(pp_range <- quantile(post_pred, 
                      probs = c(0.05, 0.95)))
       5%       95% 
 68.88551 128.75195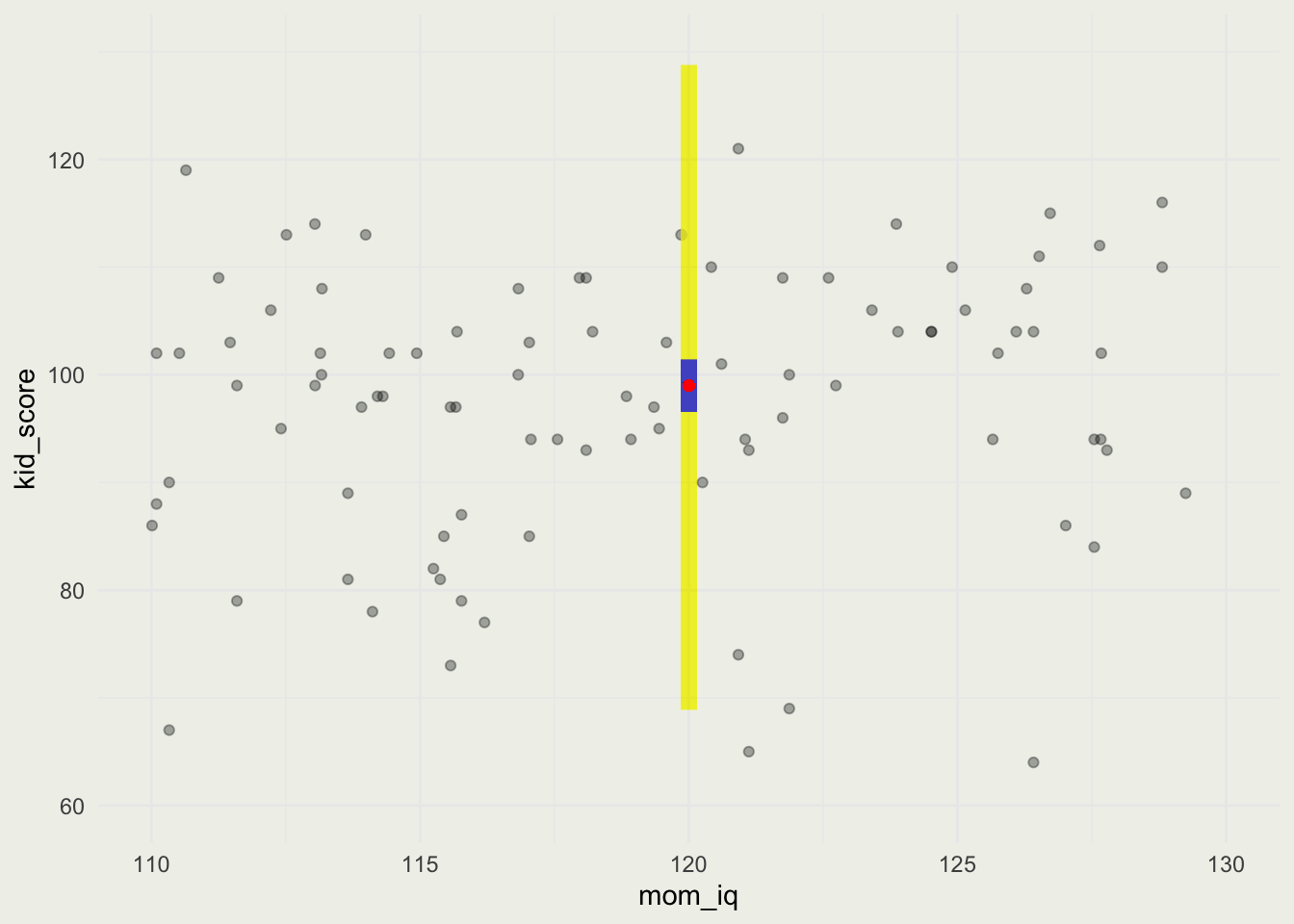

Linear Regression Assumptions

Presented in the order of importance

  • Validity of the model for the question at hand
  • Representativeness and valid scope of inference
  • Additivity and linearity
  • Independence of errors
  • Equal variance of errors
  • Normality of errors

10+ quick tips to improve your regression modeling

This advice comes from “Regression and Other Stories” by Gelman and Hill

  • Think generatively
  • Think about what you are measuring
  • Think about variation, replication
  • Forget about statistical significance
  • Graph the relevant and not the irrelevant
  • Interpret regression coefficients as comparisons
  • Understand statistical methods using fake-data simulation
  • Fit many models
  • Set up a computational workflow
  • Use transformations
  • Do causal inference in a targeted way, not as a byproduct of a large regression
  • Learn methods through live examples

Thanks for being part of my class!

  • Lectures: https://ericnovik.github.io/smac.html
  • Keep in touch:
    • eric.novik@nyu.edu
    • https://www.linkedin.com/in/enovik/
    • Twitter: @ericnovik
    • Personal blog: https://ericnovik.com/