Bayesian Inference
NYU Applied Statistics for Social Science Research
Conjugate Models and Posterior Sampling
- Gamma-Poisson family
- Normal-Normal family
- Introduction to posterior sampling on a grid
- Introduction to Stan
- Basic Markov Chain diagnostics
- Effective sample size
- Computing the R-Hat statistic
\[ \DeclareMathOperator{\E}{\mathbb{E}} \DeclareMathOperator{\P}{\mathbb{P}} \DeclareMathOperator{\V}{\mathbb{V}} \DeclareMathOperator{\L}{\mathcal{L}} \DeclareMathOperator{\I}{\text{I}} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \]
Poisson
Poisson distribution arises when we are interested in counts
In practice, we rarely use Poisson due to its restrictive nature
Poisson RV \(Y\) is paremeterized with a rate of occurance \(\lambda\): \(Y|\lambda \sim \text{Pois}(\lambda)\)
\[ f(y \mid \lambda) = \frac{e^{-\lambda} \lambda^y}{y!}\;\; \text{ for } y \in \{0,1,2,\ldots\} \]Notice, the Tailor series for \(e^\lambda = \sum_{y=0}^{\infty} \frac{\lambda^y}{y!}\) immediately validates that \(f\) is a PDF
Also, \(\E(Y | \lambda) = \V(Y | \lambda) = \lambda\), which is the restrictive case mentioned about — real count data seldom satisfied this constraint
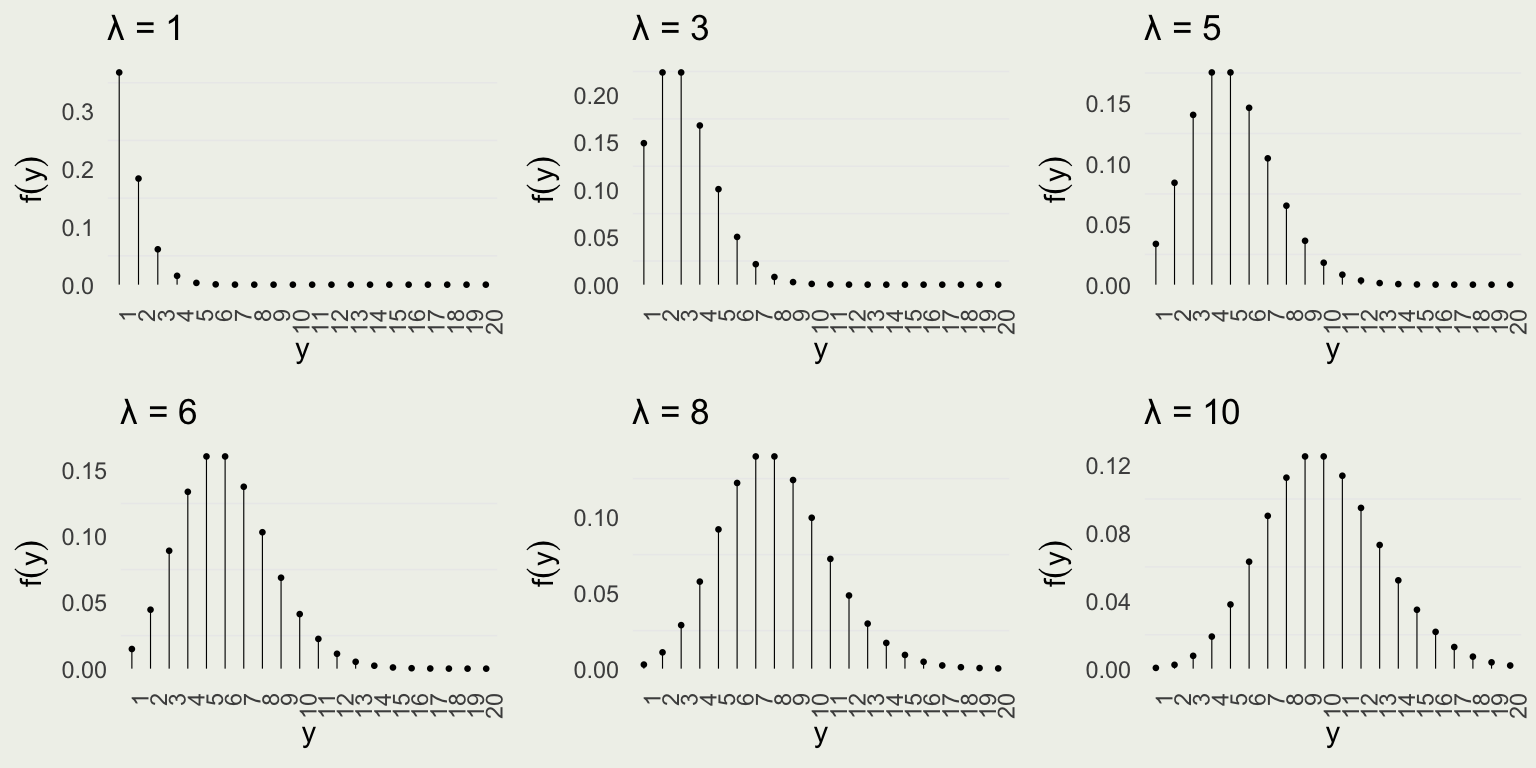
Visualizing Poission
- Notice that as the rate increases, so does the expected number of events as well as variance, which immediately follows from \(\E(Y) = \V(Y) = \lambda\)
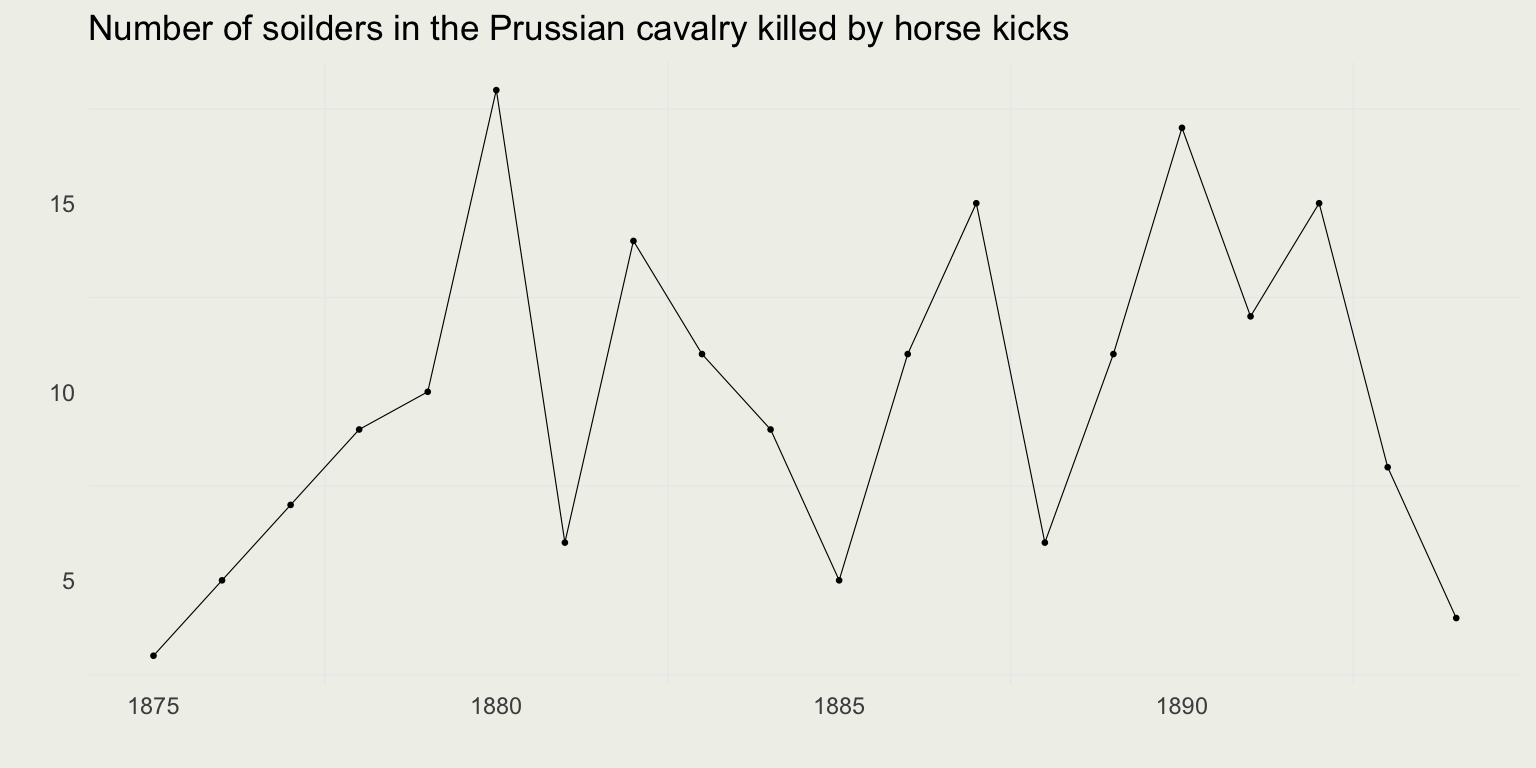
Example: Hourse Kicks
- Serving in Prussian cavalry in the 1800s was a perilous affair
- Aside from the usual dangers of military service, you were at risk of being killed by a horse kick
- Data from the book The Law of Small Numbers by Ladislaus Bortkiewicz (1898)
- Bortkiewicz was a Russian economist and statistician of Polish ancestry
Poisson Likelihood
Assume we observe \(Y_1, Y_2, ..., Y_n\) independant Poisson random variables
The joint lilelihood, a function of the parameter \(\lambda\) for \(y_i \in \mathbb{Z}^+\) and \(\lambda > 0\), is given by: \[ \begin{eqnarray} f(y \mid \lambda) & = & \prod_{i=1}^n f(y_i \mid \lambda) = f(y_1 \mid \lambda) f(y_2 \mid \lambda) \cdots f(y_n \mid \lambda) = \prod_{i=1}^{n}\frac{\lambda^{y_i}e^{-\lambda}}{y_i!} \\ & = &\frac{\lambda^{y_1}e^{-\lambda}}{y_1!} \cdot \frac{\lambda^{y_2}e^{-\lambda}}{y_2!} \cdots \frac{\lambda^{y_n}e^{-\lambda}}{y_n!} \\ & = &\frac{\left(\lambda^{y_1}\lambda^{y_2} \cdots \lambda^{y_n}\right) \left(e^{-\lambda}e^{-\lambda} \cdots e^{-\lambda}\right)}{y_1! y_2! \cdots y_n!} \\ & = &\frac{\lambda^{\sum_{i=1}^{n} y_i}e^{-n\lambda}}{\prod_{i=1}^n y_i!} \propto \lambda^{\sum_{i=1}^{n} y_i}e^{-n\lambda} \end{eqnarray} \]
We call \(\sum_{i=1}^{n} y_i\) a sufficient statistic
Conjugate Prior for Poisson
The likelihood has a form of \(\lambda^{a} e^{-b\lambda}\) so we expect the conjugate prior to be of the same form
Gamma PDF satisfied this condition: \(f(\lambda) \propto \lambda^{\alpha - 1} e^{-\beta\lambda}\)
Matching up the exponents, we can interpret \((\alpha - 1)\) as the total number of incidents \(\sum y_i\) out of \(\beta\) prior observations
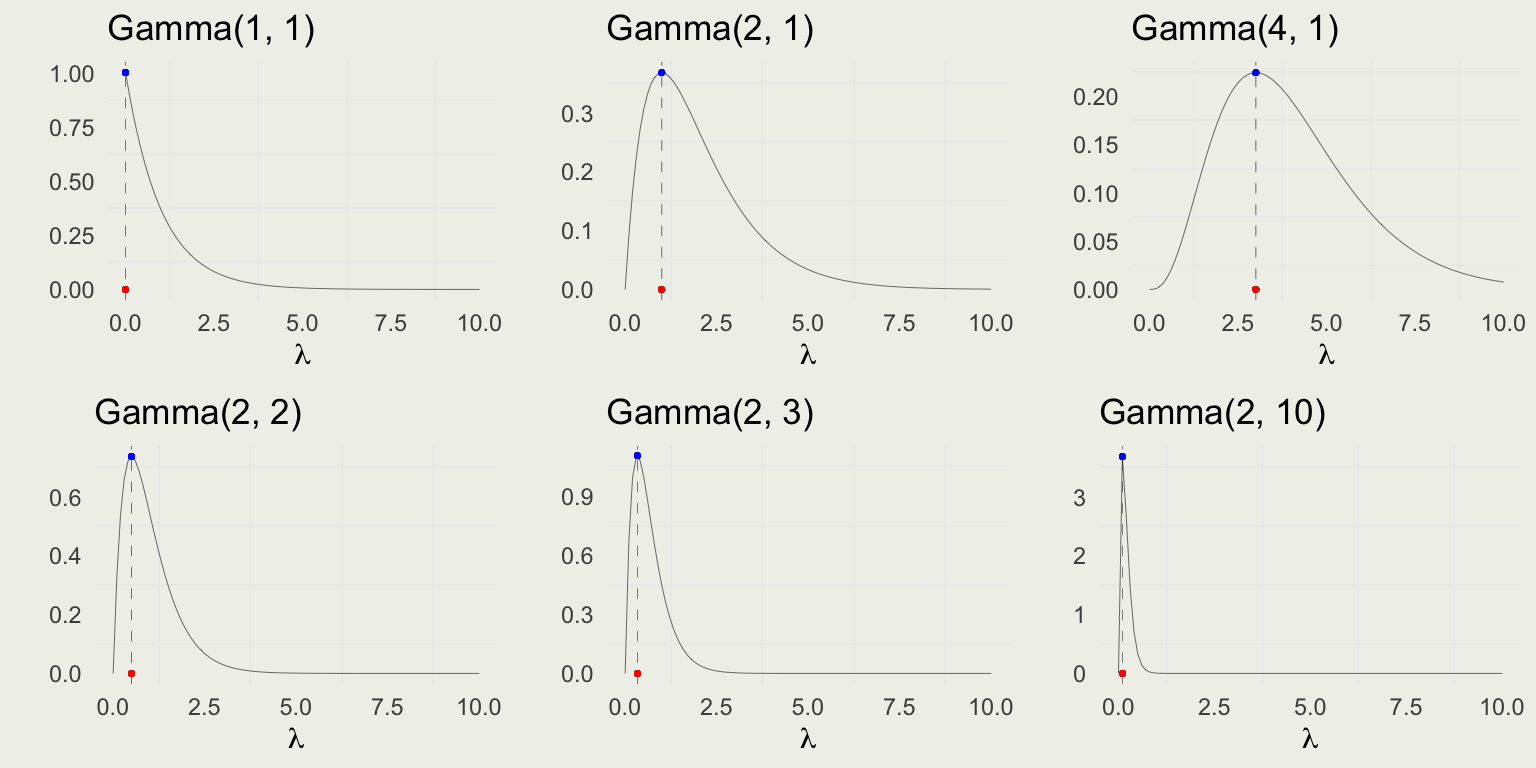
Full Gamma density is \(\text{Gamma}(\lambda|\alpha,\beta)=\frac{\beta^{\alpha}} {\Gamma(\alpha)} \, \lambda^{\alpha - 1}e^{-\beta \, \lambda}\) for \(\lambda, \alpha, \beta \in \mathbb{R}^+\) \[ \begin{equation} \begin{split} \E(\lambda) & = \frac{\alpha}{\beta} \\ \text{Mode}(\lambda) & = \frac{\alpha - 1}{\beta} \;\; \text{ for } \alpha \ge 1 \\ \V(\lambda) & = \frac{\alpha}{\beta^2} \\ \end{split} \end{equation} \]
When \(\alpha = 1\), \(\lambda \sim \text{Dist}(\beta)\). What is \(\text{Dist}\)? Work in pairs.
Visualizing Gamma
- Notice that variance, mean, and mode are increasing with \(\alpha\)
Gamma Posterior
Prior is \(f(\lambda) \propto \lambda^{\alpha - 1} e^{-\beta\lambda}\)
Likelihood is \(f(y | \lambda) \propto \lambda^{\sum_{i=1}^{n} y_i}e^{-n\lambda}\) \[ \begin{eqnarray} f(\lambda \mid y) & \propto & \text{prior} \cdot \text{likelihood} \\ & = & \lambda^{\alpha - 1} e^{-\beta\lambda} \cdot \lambda^{\sum_{i=1}^{n} y_i}e^{-n\lambda} \\ & = & \lambda^{\alpha + \sum_{i=1}^{n} y_i - 1} \cdot e^{-\beta\lambda - n\lambda} \\ & = & \lambda^{\color{red}{\alpha + \sum_{i=1}^{n} y_i} - 1} \cdot e^{-\color{red}{(\beta + n)} \lambda} \\ f(\lambda \mid y) & = & \text{Gamma}\left( \alpha + \sum_{i=1}^{n} y_i, \, \beta + n \right) \end{eqnarray} \]
As before, we can match the Gamma kernel without doing the integration
Checking the Constant
- Gamma prior integration constant: \(\frac{\beta^{\alpha}}{\Gamma(\alpha)}\)
- The posterior kernel integration constant is the reciprocal of: \(\frac{\Gamma(\alpha + \sum y_i)}{(\beta + n)^{\alpha + \sum y_i}}\). Why?
- We can sanity check this in SymPy, by integrating \(\lambda^{\color{red}{\alpha + \sum_{i=1}^{n} y_i} - 1} \cdot e^{-\color{red}{(\beta + n)} \lambda}\), and letting \(t = \sum y_i\)
\[\left(b + n\right)^{- a - t} \Gamma\left(a + t\right)\]
Posterior Mean and Variance
Posterior mean and variance follow from the updated prior mean and variance:
\[ \begin{eqnarray} \E(\lambda \mid y) &=& \frac{\alpha'}{\beta'} = \frac{\alpha + \sum_{i=1}^{n} y_i}{\beta + n} \\ \V(\lambda \mid y) &=& \frac{\alpha'}{(\beta')^2} = \frac{\alpha + \sum_{i=1}^{n} y_i}{(\beta + n)^2} \end{eqnarray} \]
Prussian Army Hourse Kicks
- From 1875 to 1894, there were 14 different cavalry corps
- Each reported a number of deaths by horse kick every year
- There are 20 years x 14 corps making 280 observations
| Year | GC | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C14 | C15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1875 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 1876 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1877 | 2 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 2 | 0 |
| 1878 | 1 | 2 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1879 | 0 | 0 | 0 | 1 | 1 | 2 | 2 | 0 | 1 | 0 | 0 | 2 | 1 | 0 |
| 1880 | 0 | 3 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 1 | 4 | 3 | 0 |
| 1881 | 1 | 0 | 0 | 2 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1882 | 1 | 2 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 2 | 1 | 4 | 1 |
Prussian Army Hourse Kicks
# this flattens the data frame into a vector
dd <- unlist(d[, -1])
p <- ggplot(aes(y), data = data.frame(y = dd))
p1 <- p + geom_histogram() +
xlab("Number of deaths reported") + ylab("") +
ggtitle("Total reported counts of deaths")
p2 <- p + geom_histogram(aes(y = ..count../sum(..count..))) +
xlab("Number of deaths reported") + ylab("") +
ggtitle("Proportion of reported counts of deaths")
grid.arrange(p1, p2, nrow = 1)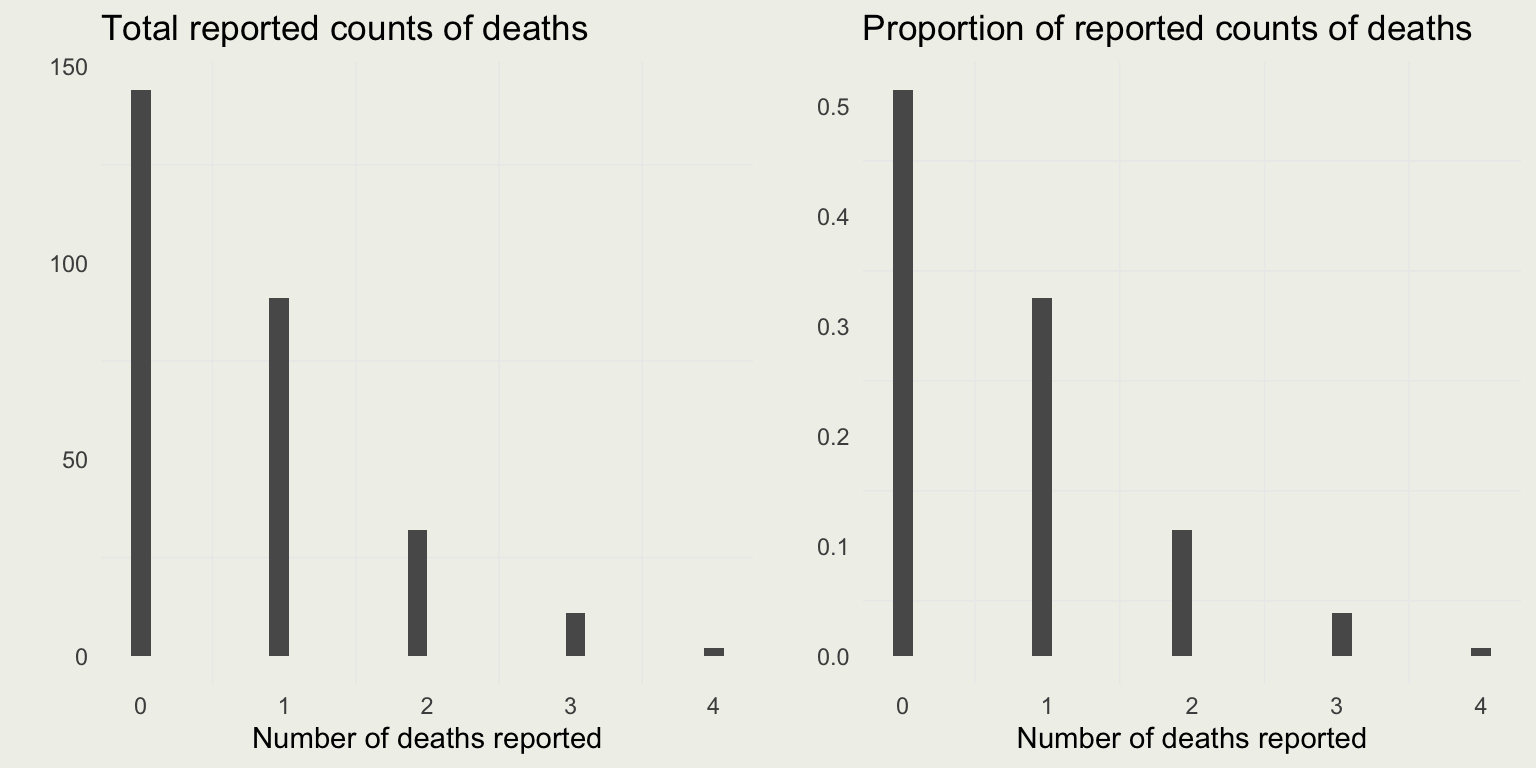
Prussian Army Hourse Kicks
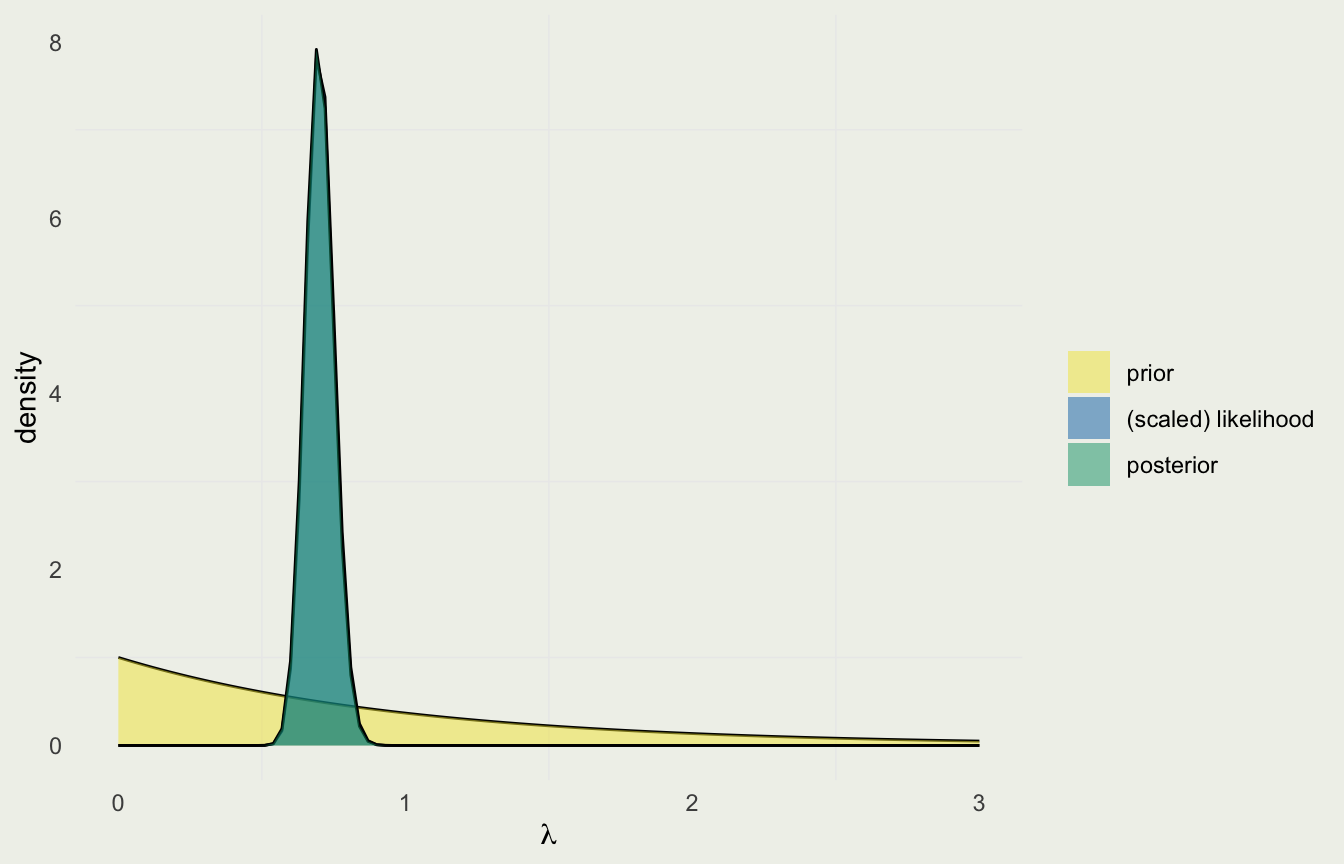
- Let’s assume that before seeing the data, your friend told you that last year, in 1874, there were no deaths reported in his corps
- That would imply \(\beta = 1\) and \(\alpha - 1 = 0\) or \(\alpha = 1\)
- The prior on lambda would therefore be \(\text{Gamma}(1, 1)\)
- The posterior is \(\text{Gamma}\left( \alpha + \sum y_i, \, \beta + N \right) = \text{Gamma}(197, \, 281)\)
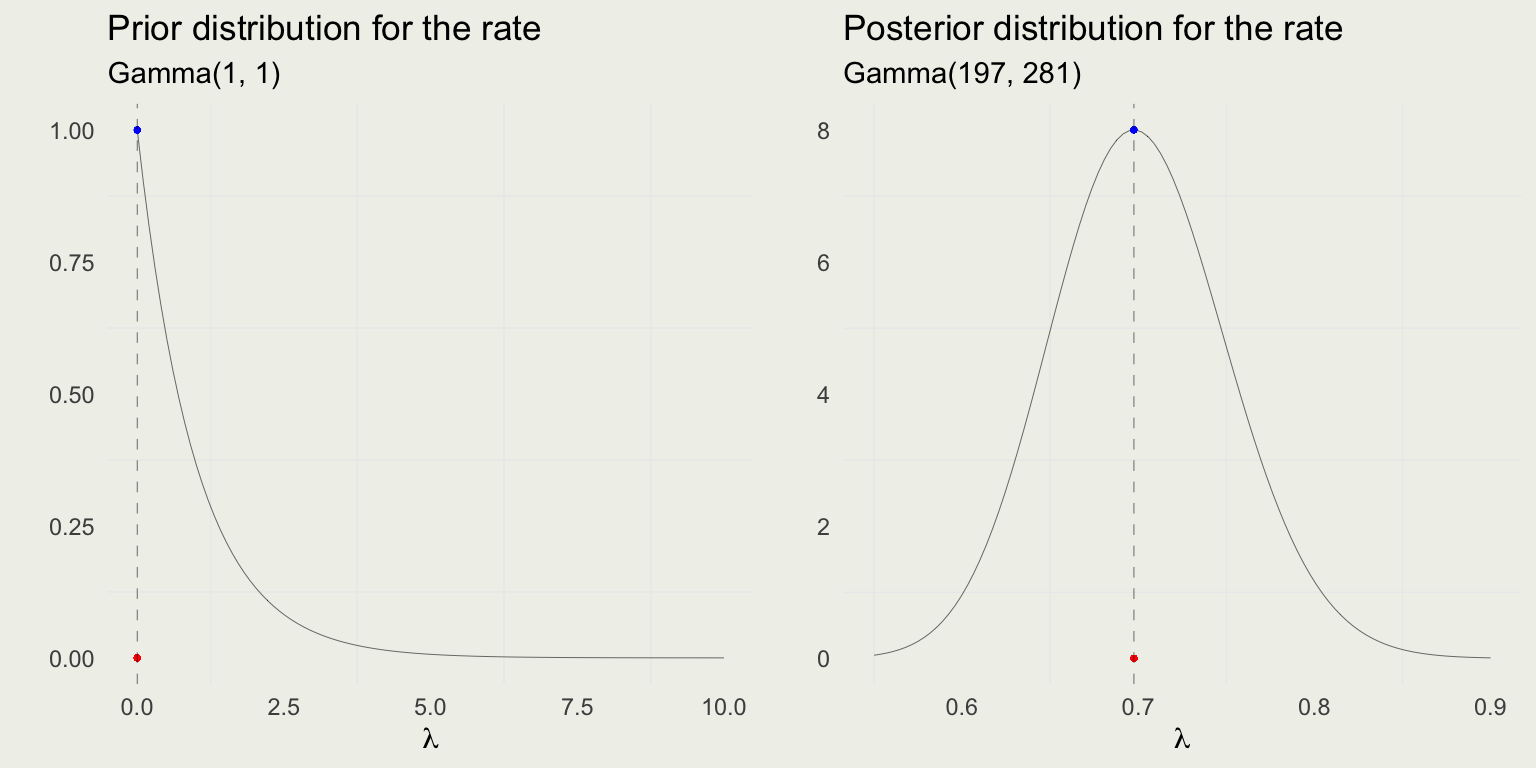
Likelihood Dominates
- With so much data relative to prior observations, the likelihood completely dominates the prior
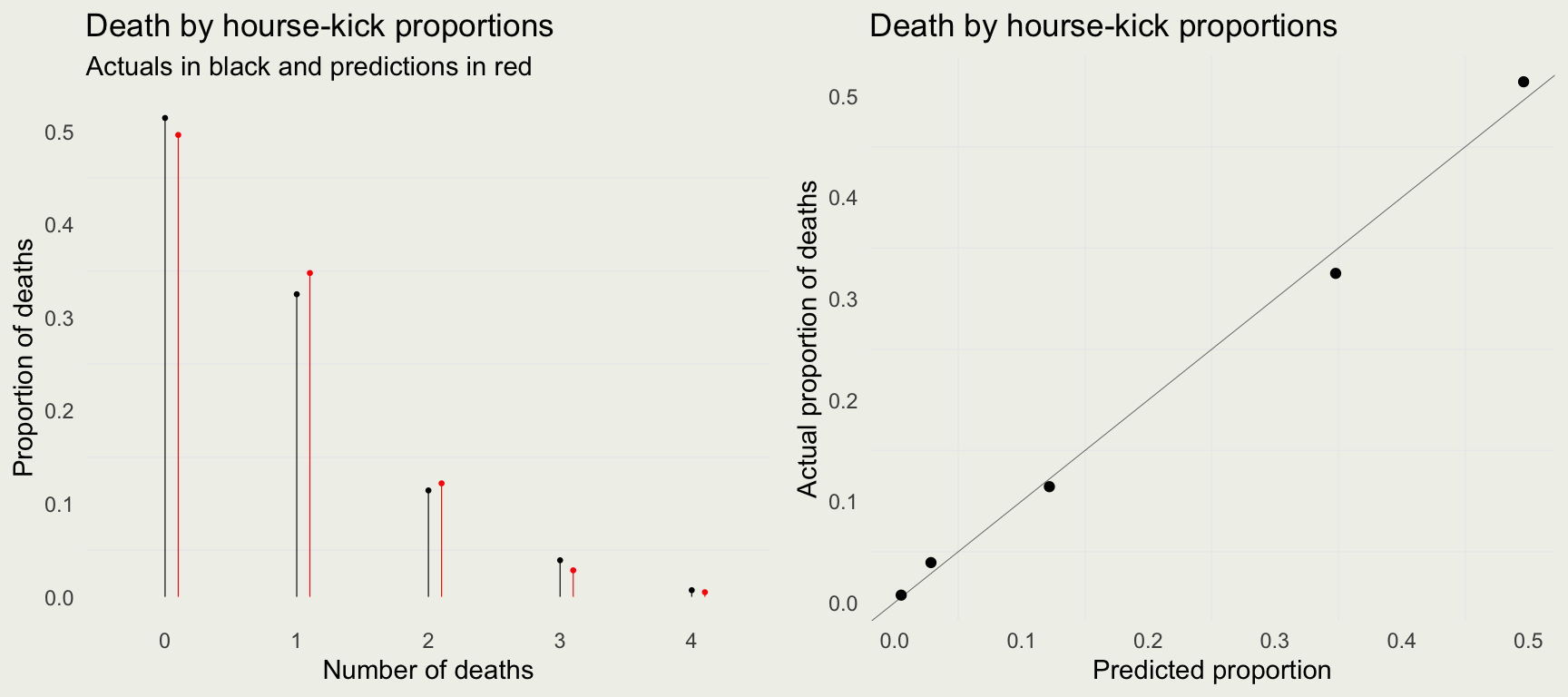
Checking the Fit
- We can plug the posterior mean for \(\lambda\) into the Poisson PMF
Adding Exposure
- Poisson likelihood seems to work well for these data
- It is likely that each of the 16 corps had about the same number of soldier-horses, a common military practice
- Suppose each corps has a different number of cavalrymen
- We need to introduce an exposure variable \(x_i\) for each corps unit \[ \begin{eqnarray} y_i & \sim & \text{Poisson}(x_i \lambda)\\ \lambda & \sim & \text{Gamma}(\alpha, \beta) \\ f(y \mid \lambda) & \propto & \lambda^{\sum_{i=1}^{n} y_i}e^{- (\sum_{i=1}^{n} x_i) \lambda} \\ f(\lambda \mid y) & = & \text{Gamma} \left( \alpha + \sum_{i=1}^{n} y_i, \, \beta + \sum_{i=1}^{n} x_i \right) \end{eqnarray} \]
Normal PDF
- The last conjugate distribution we will introduce is Normal
- We will only consider a somewhat unrealistic case of known variance \(\sigma \in \mathbb{R}^+\) and unknown mean \(\mu \in \mathbb{R}\)
- Normal PDF is for one observation \(y\) is given by: \[ \begin{eqnarray} \text{Normal}(y \mid \mu,\sigma) & = &\frac{1}{\sqrt{2 \pi} \ \sigma} \exp\left( - \, \frac{1}{2} \left( \frac{y - \mu}{\sigma} \right)^2 \right) \\ \E(Y) & = & \text{ Mode}(Y) = \mu \\ \V(Y) & = & \sigma^2 \\ \end{eqnarray} \]
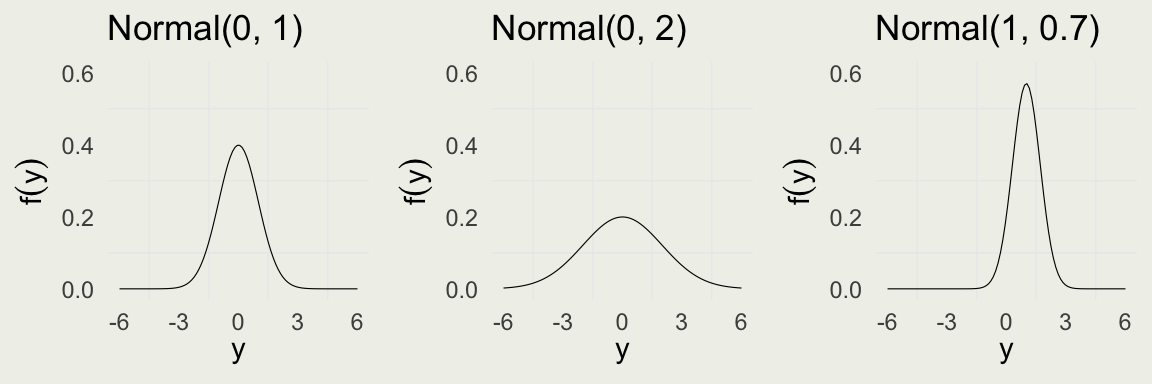
Normal PDF
- Normal arises when many independent small contributions are added up
- It is a limiting distribution of means of an arbitrary distribution
plot_xbar <- function(n_repl, n_samples) {
x <- seq(0.6, 1.4, len = 100)
xbar <- replicate(n_repl,
mean(rexp(n_samples, rate = 1)))
mu <- dnorm(x, mean = 1, sd = 1/sqrt(n_samples))
p <- ggplot(aes(x = xbar),
data = tibble(xbar))
p + geom_histogram(aes(y = ..density..),
bins = 30, alpha = 0.6) +
geom_line(aes(x = x, y = mu),
color = 'red',
linewidth = 0.3,
data = tibble(x, y)) +
ylab("") + theme(axis.text.y = element_blank())
}
p1 <- plot_xbar(1e4, 100) +
ggtitle("Sampling means from rexp(100, 1)")
p2 <- plot_xbar(1e4, 300) +
ggtitle("Sampling means from rexp(300, 1)")
grid.arrange(p1, p2, nrow = 2)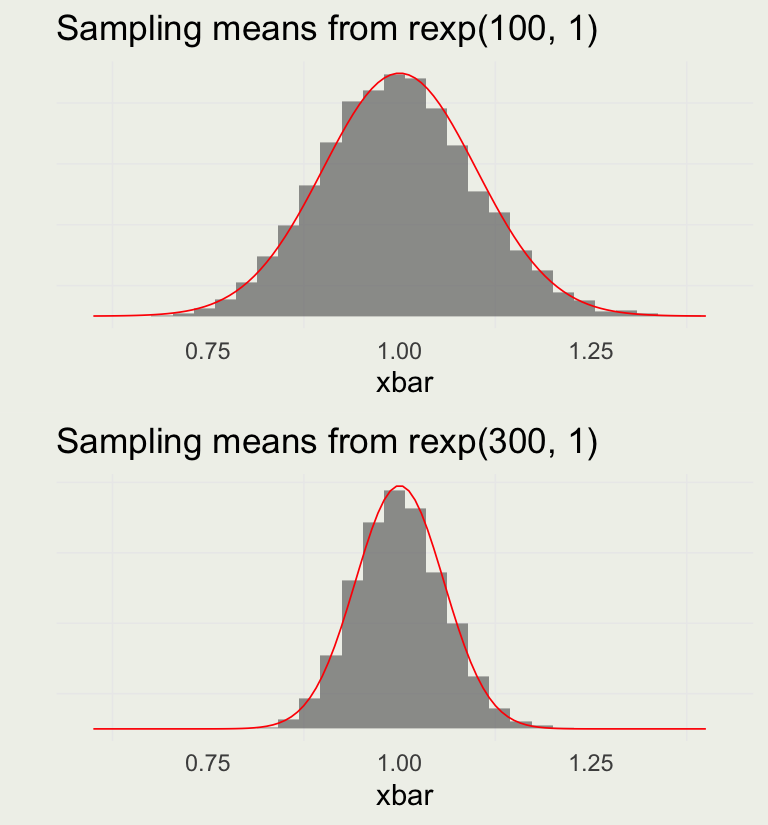
Joint Normal Likelihood
After observing data \(y\), we can compute the joint normal likelihood, assuming \(\sigma\) is known \[ \begin{eqnarray} f(y \mid \mu) & = & \prod_{i=1}^{n}\frac{1}{\sqrt{2 \pi} \ \sigma} \exp\left( - \, \frac{1}{2} \left( \frac{y_i - \mu}{\sigma} \right)^2 \right) \\ & \propto & \prod_{i=1}^{n} \exp\left( - \, \frac{1}{2} \left( \frac{y_i - \mu}{\sigma} \right)^2 \right) \\ & = & \exp \left( {-\frac{\sum_{i=1}^n(y_i-\mu)^2}{2\sigma^2}}\right) \\ &\propto& \exp\left({-\frac{(\bar{y}-\mu)^2}{2\sigma^2/n}}\right) \end{eqnarray} \]
The last line is derived by expanding the square and dropping terms that don’t depend on \(\mu\); \(\bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i\)
Expansion: \(\sum_{i=1}^n (y_i - \mu)^2 = \sum_{i=1}^n \left[(y_i - \bar{y}) + (\bar{y} - \mu)\right]^2\)
Normal Prior
- We can now define the prior on \(\mu\)
- We will choose \(\mu\) to be normal: \(\mu \sim \text{Normal}(\theta, \tau^2)\) \[ \begin{eqnarray} f(\mu \mid \theta, \tau) & \propto & \exp\left( - \, \frac{1}{2} \left( \frac{\mu - \theta}{\tau} \right)^2 \right) \\ \end{eqnarray} \]
Normal Posterior
- For one observation \(y\):
\[ \begin{eqnarray} f(y \mid \mu) & \propto & \exp\left( - \, \frac{1}{2} \left( \frac{y - \mu}{\sigma} \right)^2 \right) \\ f(\mu) & \propto & \exp\left( - \, \frac{1}{2} \left( \frac{\mu - \theta}{\tau} \right)^2 \right) \\ f(\mu \mid y) & \propto & \exp\left( - \, \frac{1}{2} \left( \frac{\mu - \theta}{\tau} \right)^2 - \frac{1}{2} \left( \frac{y - \mu}{\sigma} \right)^2 \right) \\ & = & \exp \left( -\frac{1}{2} \left( \frac{(\mu - \theta)^2}{\tau^2} + \frac{(y - \mu)^2}{\sigma^2} \right)\right) \\ & = & \exp \left( -\frac{1}{2\tau_1^2} \left( \mu - \mu_1 \right)^2 \right) \end{eqnarray} \]
Normal Posterior
For one observation: \[ \begin{eqnarray} f(\mu \mid y) &\propto& \exp \left( -\frac{1}{2\tau_1^2} \left( \mu - \mu_1 \right)^2 \right) \text{ i.e. } \mu \mid y \sim \text{Normal}(\mu_1, \tau_1) \\ \mu_1 &=& \frac{\frac{1}{\tau^2} \theta + \frac{1}{\sigma^2} y}{\frac{1}{\tau^2} + \frac{1}{\sigma^2}} \\ \frac{1}{\tau_1^2} &=& \frac{1}{\tau^2} + \frac{1}{\sigma^2} \end{eqnarray} \]
For multiple observations: \[ \mu_1 = \frac{\frac{1}{\tau^2} \theta + \frac{n}{\sigma^2} \overline{y}}{\frac{1}{\tau^2} + \frac{n}{\sigma^2}} \\ \frac{1}{\tau_1^2} = \frac{1}{\tau^2} + \frac{n}{\sigma^2} \]
Posterior Simulation
Arianna Rosenbluth Dies at 93, The New York Times
Grid approximation
- Most posterior distributions do not have an analytical form
- In those cases, we must resort to sampling methods
- Sampling in high dimensions requires specialized algorithms
- Here, we will look at one-dimensional sampling on a grid (of parameter values)
- At the end of this lecture, we look at some output of a state-of-the-art HMC NUTS sampler
- Next week, we will examine the Metropolis-Hastings-Rosenbluth algorithm
An example of Gibbs sampling of a Bivariate Normal by Aki Vehtari and Markus Paasiniemi. 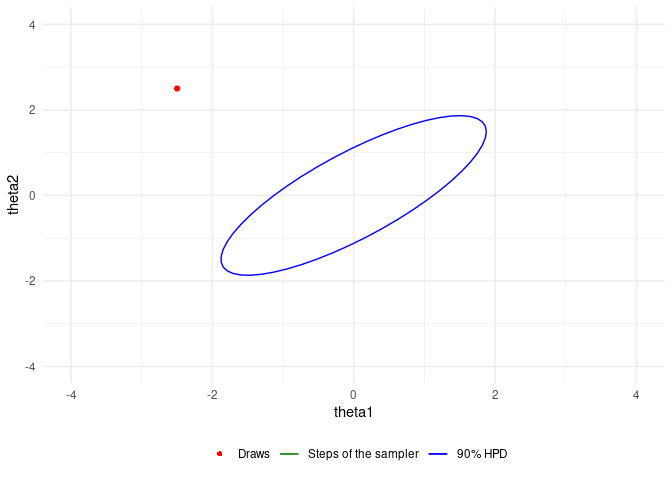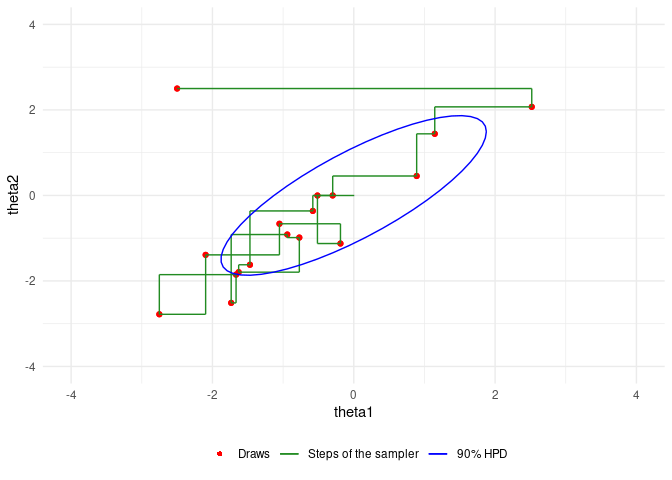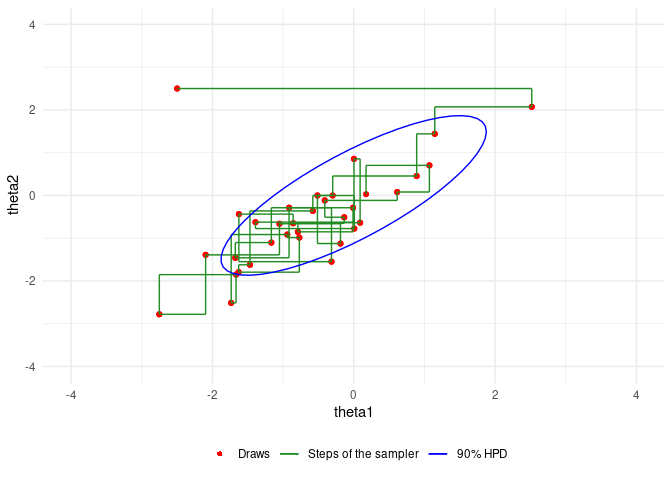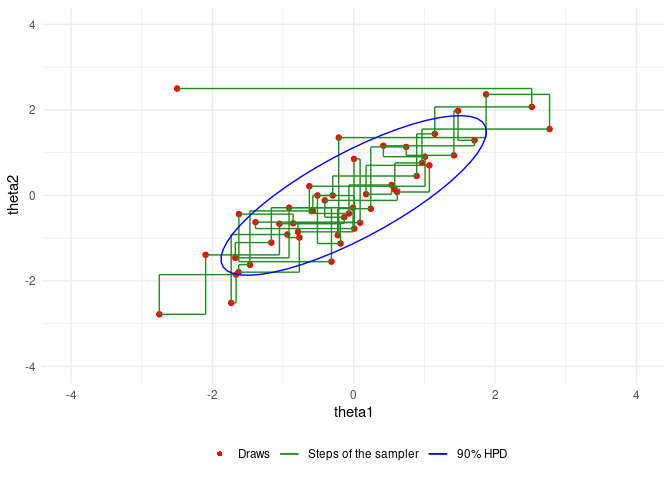
Grid approximation
- We already saw how given samples from the target distribution, we could compute quantities of interest
- The grid approach to getting samples:
- Generate discreet points in parameter space \(\theta\)
- Define our likelihood function \(f(y|\theta)\) and prior \(f(\theta)\)
- For each point on the grid, compute the product \(f(y|\theta)f(\theta)\)
- Normalize the product to sum to 1
- Sample from the resulting distribution in proportion to the posterior probability
- Here, \(\theta\) is continuous, so we can not use the technique we used for a discrete, one-dimensional prior from the clinical trial example.
- What are some limitations of this approach?
Back to the Binomial
- For simplicity we will assume uniform \(\text{Beta}(1, 1)\) prior \[ \begin{eqnarray} f(\theta)f(y\mid \theta) &\propto& \theta^{a -1}(1 - \theta)^{b-1} \cdot \prod_{i=1}^{n} \theta^{y_i} (1 - \theta)^{1 - y_i} \\ &=& \theta^0(1 - \theta)^0 \cdot \prod_{i=1}^{n} \theta^{y_i} (1 - \theta)^{1 - y_i} \\ &=& \prod_{i=1}^{n} \theta^{y_i} (1 - \theta)^{1 - y_i} \\ &=& \theta^{\sum_{i=1}^{n} y_i} \cdot (1 - \theta)^{\sum_{i=1}^{n} (1- y_i)} \end{eqnarray} \]
- On the log scale: \(\log f(\theta, y) \propto \log(\theta) \cdot\sum_{i=1}^{n} y_i + \log(1 - \theta) \cdot\sum_{i=1}^{n} (1-y_i)\)
- Suppose that 3 out of 5 patients responded to treatment
- Model: \(\text{lp}(\theta) = \log(\theta) \cdot\sum_{i=1}^{n} y_i + \log(1 - \theta) \cdot\sum_{i=1}^{n} (1-y_i)\)
lp <- function(theta, data) {
# log(theta) * sum(data$y) + log(1 - theta) * sum(1 - data$y)
lp <- 0
for (i in 1:data$N) {
lp <- lp + log(theta) * data$y[i] + log(1 - theta) * (1 - data$y[i])
}
return(lp)
}
data <- list(N = 5, y = c(0, 1, 1, 0, 1))
# generate theta parameter grid
theta <- seq(0.01, 0.99, len = 100)
# compute log likelihood and prior for every value of the grid
log_lik <- lp(theta, data); log_prior <- log(dbeta(theta, 1, 1))
# compute log posterior
log_post <- log_lik + log_prior
# convert back to the original scale and normalize
post <- exp(log_post); post <- post / sum(post)
# sample theta in proportion to the posterior probability
draws <- sample(theta, size = 1e5, replace = TRUE, prob = post)Monte Carlo Integration and MCMC
We already saw a special case of MC integration
Suppose we can draw samples from PDF \(f\), \((\theta^{(1)}, \theta^{(2)},..., \theta^{(N)})\)
If we want to compute an expectation of some function \(h\): \[ \begin{eqnarray} \E_f[h(\theta)] &=& \int h(\theta)f(\theta)\, d\theta &\approx& \frac{1}{N} \sum_{i = 1}^{N} h \left( \theta^{(i)} \right) \end{eqnarray} \]
The Law of Large Numbers tells us that these approximations improve with \(N\)
In practice, the challenge is obtaining draws from \(f\)
That’s where MCMC comes in
- Suppose we want to estimate the mean and variance of standard normal
- In case of the mean, \(h(\theta) := \theta\) and variance, \(h(\theta) := \theta^2\), and \(f(\theta) = \frac{1}{\sqrt{2 \pi} \ } e^{-\theta^2/2}\) \[ \begin{eqnarray} \E[\theta] &=& \int_{-\infty}^{\infty} \theta f(\theta)\, d\theta &\approx& \frac{1}{N} \sum_{i = 1}^{N} \theta^{(i)} \\ \E[\theta^2] &=& \int_{-\infty}^{\infty} \theta^2 f(\theta)\, d\theta &\approx& \frac{1}{N} \sum_{i = 1}^{N} \left( \theta^{(i)} \right)^2 \end{eqnarray} \]
- Suppose we want to estimate a CDF of Normal(0, 1) at some point \(t\)
- We let \(h(\theta) = \I(\theta < t)\), where \(\I\) is an indicator function that returns 1 when \(\theta < t\) and \(0\) otherwise \[ \begin{eqnarray} \E[h(\theta)] = \E[\I(\theta < t)] &=& \int_{-\infty}^{\infty} \I(\theta < t) f(\theta)\, d\theta = \int_{-\infty}^{t}f(\theta)\, d\theta = \Phi(t) \\ &\approx& \frac{1}{N} \sum_{i = 1}^{N} \I(\theta^{(i)} < t) \\ \end{eqnarray} \]
- MCMC is a very general method for computing expectations (integrals)
- It produces dependant (autocorrelated) samples, but for a good algorithm, the dependence is manageable
- Stan’s MCMC algorithm is very efficient (more on that later) and requires all parameters to be continuous (data can be discrete)
- It solves the problem of drawing from distribution \(f(\theta)\) where \(f\) is not one of the fundamental distributions and \(\theta\) is high dimentional
- What is high-dimensional? Modern algorithms like NUTS can jointly sample tens of thousands and more parameters
- That’s 10,000+ dimensional integrals of complicated functions!
Introduction to Stan
- Stan is a procedural, statically typed, Turning complete, probabilistic programming language
- Stan language expresses a probabilistic model
- Stan transpiler converts it to C++
- Stan inference algorithms perform parameter estimation
- Our model: \(\text{lp}(\theta) = \log(\theta) \cdot\sum_{i=1}^{n} y_i + \log(1 - \theta) \cdot\sum_{i=1}^{n} (1-y_i)\)
Running Stan
library(cmdstanr)
m1 <- cmdstan_model("stan/01-bernoulli.stan") # compile the model
data <- list(N = 5, y = c(0, 1, 1, 0, 1))
f1 <- m1$sample( # for other options to sample, help(sample)
data = data, # pass data as a list, match the vars name to Stan
seed = 123, # to reproduce results, Stan does not rely on R's seed
chains = 4, # total chains, the more, the better
parallel_chains = 4, # for multi-processor CPUs
refresh = 0, # number of iterations printed on the screen
iter_warmup = 500, # number of draws for warmup (per chain)
iter_sampling = 500 # number of draws for samples (per chain)
)Running MCMC with 4 parallel chains...
Chain 1 finished in 0.0 seconds.
Chain 2 finished in 0.0 seconds.
Chain 3 finished in 0.0 seconds.
Chain 4 finished in 0.0 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.0 seconds.
Total execution time: 0.3 seconds.# A tibble: 2 × 10
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 lp__ -5.30 -5.02 0.734 0.320 -6.82 -4.78 1.00 800. 1024.
2 theta 0.566 0.577 0.173 0.187 0.273 0.833 1.01 860. 986.Working With Posterior Draws
# A tibble: 6 × 5
# Groups: .variable [1]
.chain .iteration .draw .variable .value
<int> <int> <int> <chr> <dbl>
1 4 495 1995 lp__ -4.84
2 4 496 1996 lp__ -4.85
3 4 497 1997 lp__ -4.83
4 4 498 1998 lp__ -5.04
5 4 499 1999 lp__ -4.78
6 4 500 2000 lp__ -4.78# A tibble: 2 × 2
.variable mean
<chr> <dbl>
1 lp__ -5.30
2 theta 0.566# A tibble: 2 × 7
.variable .value .lower .upper .width .point .interval
<chr> <dbl> <dbl> <dbl> <dbl> <chr> <chr>
1 lp__ -5.02 -6.82 -4.78 0.9 median qi
2 theta 0.577 0.273 0.833 0.9 median qi # A tibble: 6 × 5
.chain .iteration .draw theta lp__
<int> <int> <int> <dbl> <dbl>
1 4 495 1995 0.505 -4.84
2 4 496 1996 0.503 -4.85
3 4 497 1997 0.510 -4.83
4 4 498 1998 0.436 -5.04
5 4 499 1999 0.568 -4.78
6 4 500 2000 0.582 -4.78theta <- seq(0.01, 0.99, len = 100)
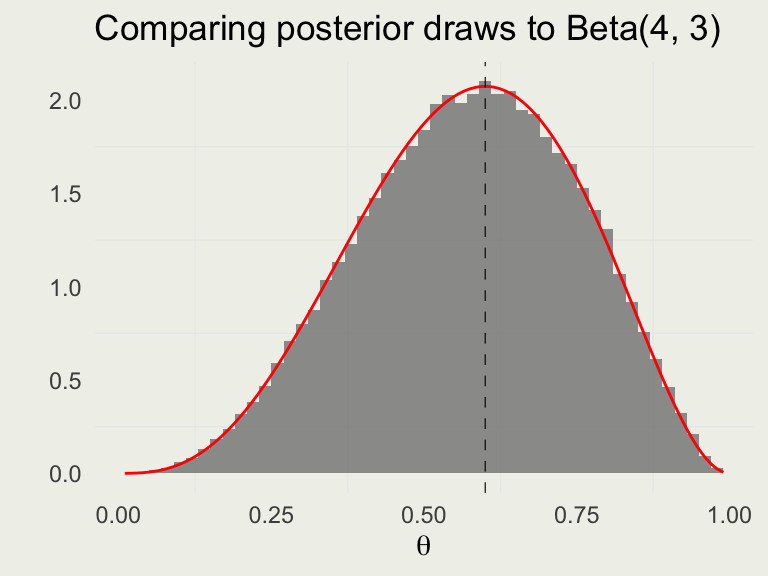
p <- ggplot(aes(theta), data = draws)
p + geom_histogram(aes(y = after_stat(density)),
bins = 30, alpha = 0.6) +
geom_line(aes(theta, beta_dens),
linewidth = 0.5, color = 'red',
data = tibble(theta, beta_dens)) +
ylab("") + xlab(expression(theta)) +
ggtitle("Posterior draws from Stan")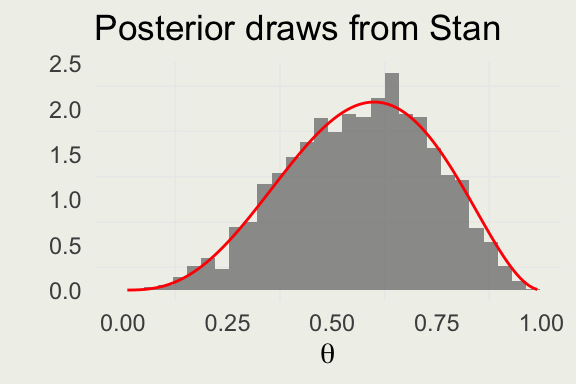
What’s a Chain
A is a sequence of random variables \(\{X_n\}_{n \geq 0}\) defined on a state space \(S\) such that for all \(n \geq 0\) and for any states \(i_0, i_1, \dots, i_{n+1} \in S\), the Markov property holds:
\[ \mathbb{P}(X_{n+1}=j \mid X_0=i_0, X_{n-1}=i_{n-1}, \dots, X_n=i_n) = \mathbb{P}(X_{n+1}=j \mid X_n=i) \]
The transition probabilities are represented by a matrix \(Q\), where:
\[ q_{ij} = \mathbb{P}(X_{n+1} = j \mid X_n = i) \]
Dynamic Simulation
MCMC Diagnostics
- In general, you want to assess (1) the quality of the draws and (2) the quality of predictions
- There are no guarantees in either case, but the former is easier than the latter
- The folk theorem of statistical computing: computational problems often point to problems in the model (AG)
- We will address the quality of the draws now and the quality of predictions later in the course
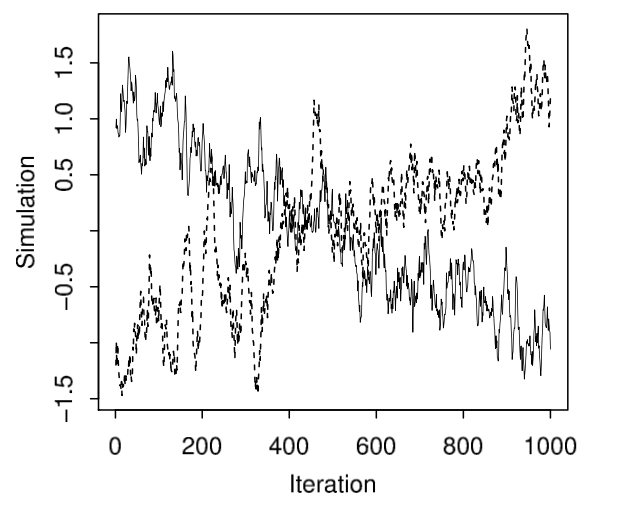
Example of bad markov chains, page 283, Figure 11.3, BDA 3. 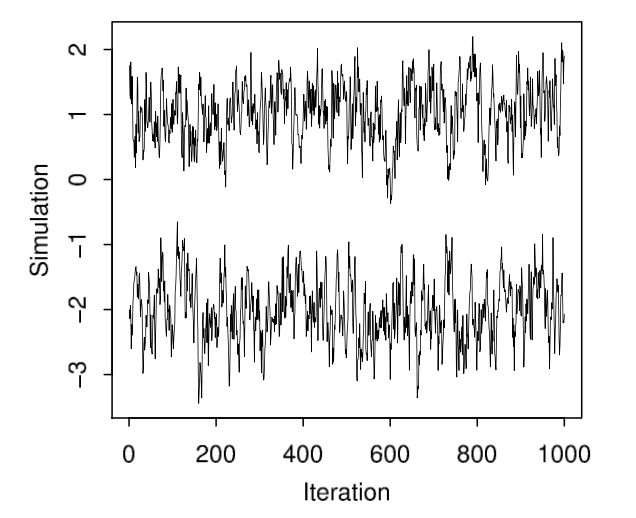
Good Chain Bad Chain
library(bayesplot)
draws <- f1$draws("theta")
color_scheme_set("viridis")
p1 <- mcmc_trace(draws, pars = "theta") + ylab(expression(theta)) +
ggtitle("Good Chain")
bad_post <- readRDS("data/bad_post.rds")
bad_draws <- bad_post$draws("mu")
p2 <- mcmc_trace(bad_draws, pars = "mu") + ylab(expression(theta)) +
ggtitle("Bad Chain")
grid.arrange(p1, p2, nrow = 2)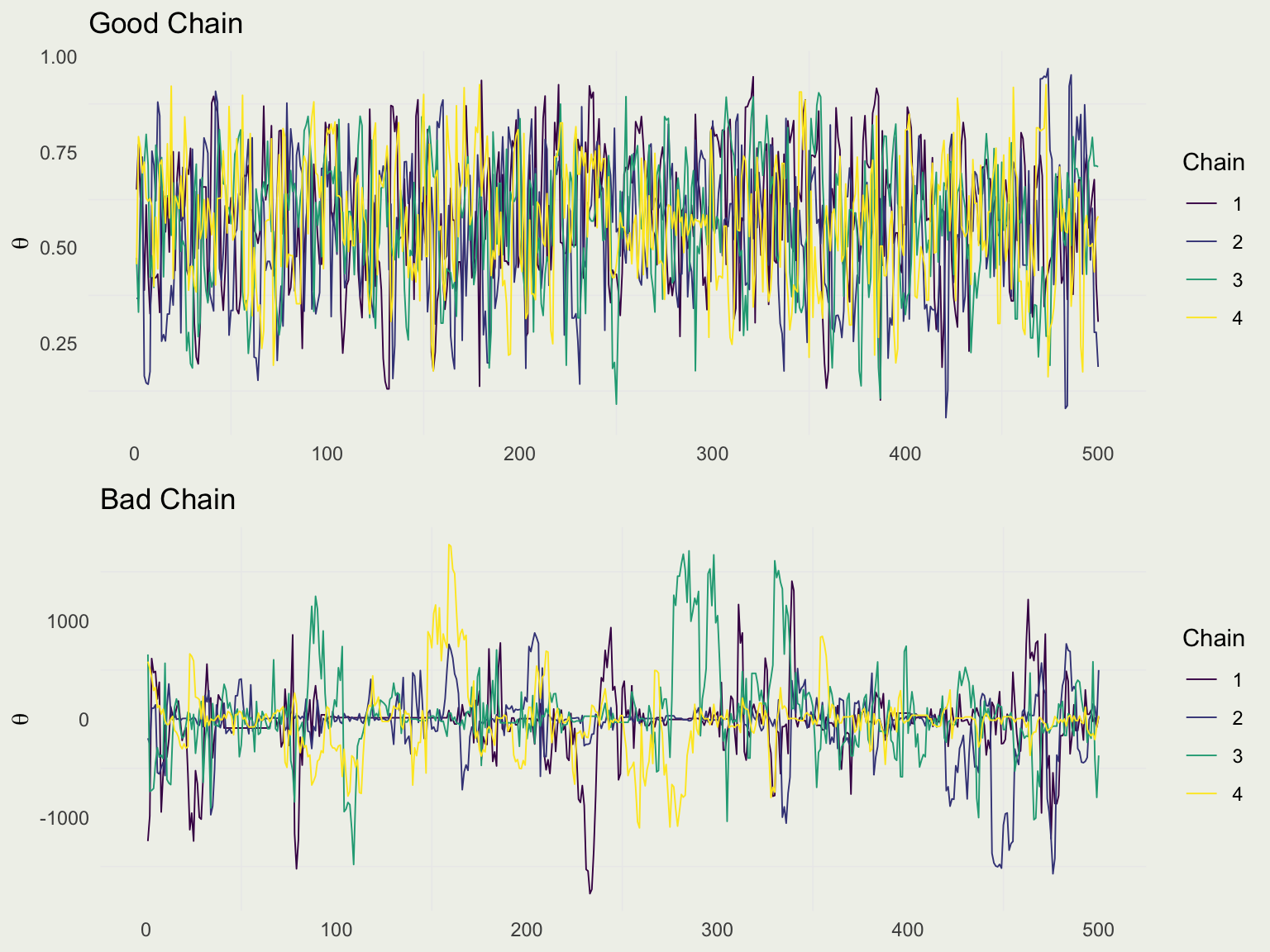
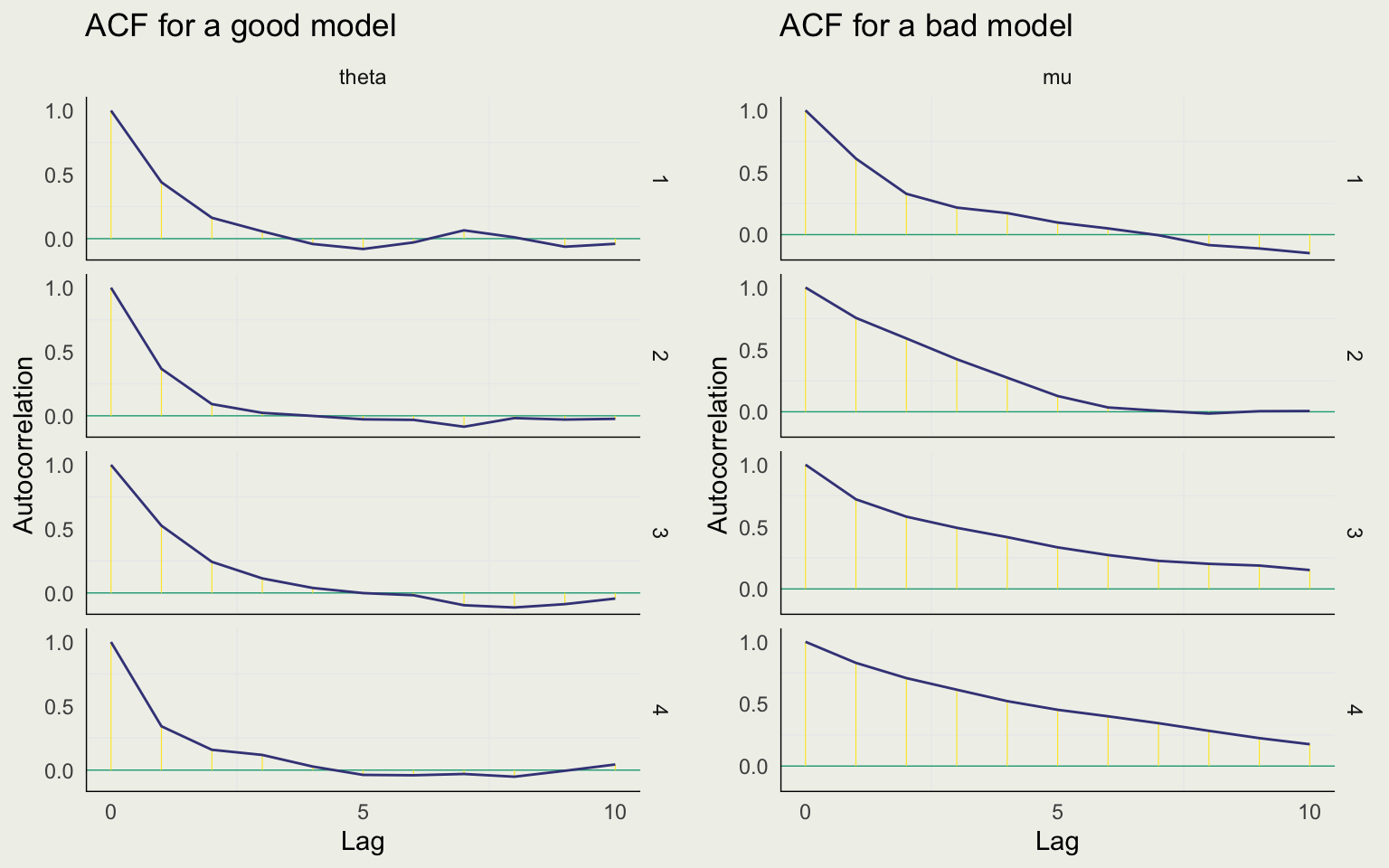
Effective Sample Size and Autocorrelation
- MCMC generates dependent draws from the target distribution
- Dependent samples are less efficient as you need more of them to estimate the quantity of interest
- ESS or \(N_{eff}\) is approximately how many independent samples you have
- Typically, \(N_{eff} < N\) for MCMC, as there is some autocorrelation
- ESS should be considered relative to \(N\): \(\frac{N_{eff}}{N}\)
- Generally, we don’t like to see \(\text{ratio} < 0.10\)
Computing R-Hat
Autocorrelation assesses the quality of a single chain
Split R-Hat estimates the extent to which the chains are consistent with one another
It does it by assessing the mixing of chains by comparing variances within and between chains (technically sequences, as chains are split up) \[ \begin{eqnarray} \hat{R} = \sqrt{\frac{\frac{n-1}{n}\V_W + \frac{1}{n}\V_B}{\V_W}} = \sqrt{\frac{\V_{\text{total}}}{\V_{W}}} \end{eqnarray} \]
\(\V_W\) is within chain variance and \(\V_B\) is between chain variance
We don’t like to see R-hats greater than 1.02 and really don’t like them greater than 1.05
Stan Homework
- Modify the program to incorporate Beta(2, 2) without using theta ~ beta(2, 2) (i.e. using target +=)
- Modify the program to account for an arbitrary Beta(a, b) distribution
- Verify that you got the right result in #1 by a) comparing Stan’s posterior means and posterior standard deviations to the means and standard deviations under the conjugate model; b) modifying the Stan program using beta(2, 2) prior and Bernoulli likelihood shown here; c) modifying the R code to get a third point of comparison.
- Hint: For #2, pass parameters a and b in the data block